题目内容
1.若正比例函数y=-2x的图象与一次函数y=x+m的图象交于点A,且点A的横坐标为-3.(1)求该一次函数的解析式;
(2)直接写出方程组$\left\{\begin{array}{l}{y=-2x}\\{y=x+m}\end{array}\right.$的解.
分析 (1)先将x=-3代入y=-2x,求出y的值,得到点A坐标,再将点A坐标代入y=x+m,利用待定系数法可得一次函数的解析式;
(2)方程组的解就是正比例函数y=-2x的图象与一次函数y=x+m的交点,根据交点坐标即可写出方程组的解.
解答 解:(1)将x=-3代入y=-2x,得y=6,
则点A坐标为(-3,6).
将A(-3,6)代入y=x+m,得-3+m=6,
解得m=9,
所以一次函数的解析式为y=x+9;
(2)方程组$\left\{\begin{array}{l}{y=-2x}\\{y=x+m}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-3}\\{y=6}\end{array}\right.$.
点评 此题主要考查了一次函数与二元一次方程(组)的关系及待定系数法求解析式,难度适中.

练习册系列答案
相关题目
2.点P(3,-4)关于y轴的对称点P′的坐标是( )
| A. | (-3,-4) | B. | (3,4) | C. | (-3,4) | D. | (-4,3) |
10.某校乐器社团成员的年龄有12,13,14,15四种,统计结果如下表:
根据表中信息判断该校乐器社团成员的平均年龄为14岁.
| 年龄/岁 | 12 | 13 | 14 | 15 |
| 人数/人 | 2 | 4 | 6 | 8 |
11. 如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
 如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )| A. | x=3 | B. | x=0 | C. | x=-2 | D. | x=-3 |
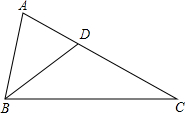 如图,已知BD是∠ABC的角平分线,且∠C=∠DBC,∠BDA=72°,求△ABC各内角度数.
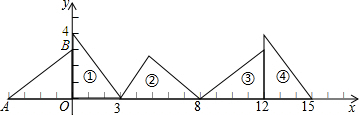
如图,已知BD是∠ABC的角平分线,且∠C=∠DBC,∠BDA=72°,求△ABC各内角度数. 如图,在平面直角坐标系xOy中,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴,交直线y=$\frac{1}{2}$x于点B1,以A1为直角顶点,A1B1为直角边,在A1B1的右侧作等腰直角三角形A1B1C1;再过点C1作A2B2∥y轴,分别交直线y=x和y=$\frac{1}{2}$x于A2,B2两点,以A2为直角顶点,A2B2为直角边,在A2B2的右侧作等腰直角三角形A2B2C2…,按此规律进行下去,点C1的横坐标为3,点C2的横坐标为$\frac{9}{2}$,点Cn的横坐标为2×($\frac{3}{2}$)n.(用含n的式子表示,n为正整数)
如图,在平面直角坐标系xOy中,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴,交直线y=$\frac{1}{2}$x于点B1,以A1为直角顶点,A1B1为直角边,在A1B1的右侧作等腰直角三角形A1B1C1;再过点C1作A2B2∥y轴,分别交直线y=x和y=$\frac{1}{2}$x于A2,B2两点,以A2为直角顶点,A2B2为直角边,在A2B2的右侧作等腰直角三角形A2B2C2…,按此规律进行下去,点C1的横坐标为3,点C2的横坐标为$\frac{9}{2}$,点Cn的横坐标为2×($\frac{3}{2}$)n.(用含n的式子表示,n为正整数)