题目内容
12.如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依次得到三角形(1))、(2)、(3)、(4)、…,那么第(12)个三角形的直角顶点的坐标是(48,0).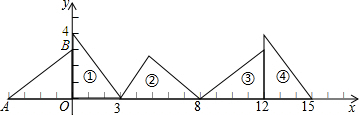
分析 观察不难发现,每三次旋转为一个循环组依次循环,第7个直角三角形的直角顶点与第6个直角三角形的直角顶点重合,然后求出一个循环组旋转过的距离,即可得解.
解答 解:由图可知,第4个三角形与第1个三角形的所处形状相同,即每三次旋转为一个循环组依次循环,
∵一个循环组旋转过的长度为12,
∴12×12÷3=48,
∴第(12)个三角形的直角顶点坐标是(48,0).
故答案为:(48,0).
点评 本题考查了坐标与图形变化-旋转,是对图形变化规律,观察出每三次旋转为一个循环组依次循环,并且下一组的第一个直角三角形与上一组的最后一个直角三角形的直角顶点重合是解题的关键.

练习册系列答案
相关题目
7.当k>0,y<0时,反比例函数y=$\frac{k}{x}$的图象在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知直线l1:y=-$\frac{2}{3}$x+$\frac{2}{3}$a与直线l2:y=$\frac{3}{2}$x-$\frac{a-1}{2}$的交点在第二象限,则a的取值范围是( )
| A. | -$\frac{1}{2}$<a<$\frac{3}{7}$ | B. | a>-$\frac{1}{2}$ | C. | a$<\frac{3}{7}$ | D. | -$\frac{1}{2}$≤a≤$\frac{3}{7}$ |