题目内容
9．正八边形不能单独铺满地面，其原因是它每个内角是135°，而360°不是这个度数的整数倍，拼接有缝隙．分析 几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．
解答 解：正八边形不能单独铺满地面，其原因是它每个内角是135°，而360°不是这个度数的整数倍，拼接有缝隙．
故答案为：135，360．
点评 本题考查平面密铺的知识，注意掌握用一种正多边形镶嵌，只有正三角形，正四边形，正六边形三种正多边形能镶嵌成一个平面图案．
练习册系列答案
相关题目
10．下列调查中，最适合采用普查方式的是（ ）
| A． | 对我县青龙河流城水质情况的调查 | |
| B． | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C． | 对一批节能灯管使用寿命的调查 | |
| D． | 对全县八年级学生视力情况的调查 |
17．已知直线l1：y=-$\frac{2}{3}$x+$\frac{2}{3}$a与直线l2：y=$\frac{3}{2}$x-$\frac{a-1}{2}$的交点在第二象限，则a的取值范围是（ ）
| A． | -$\frac{1}{2}$＜a＜$\frac{3}{7}$ | B． | a＞-$\frac{1}{2}$ | C． | a$＜\frac{3}{7}$ | D． | -$\frac{1}{2}$≤a≤$\frac{3}{7}$ |
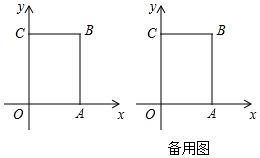如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a，b满足|a-4|+$\sqrt{b-6}$=0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动．
19．若把分式$\frac{2xy}{x+y}$（x，y为正数）中的x，y分别扩大为原来的2倍，则分式的值是（ ）
| A． | 扩大为原来的2倍 | B． | 缩小为原来的2倍 | C． | 扩大为原来的4倍 | D． | 不变 |