题目内容
18. 如图,平面直角坐标系中,一直线l分别交x轴、y轴于点B,C,过点C作直线l的垂线交x轴于点A.若点A的坐标为(2,0)且AC=4,则在直线l上是否存在点P,使△PAB与△BOC相似?若存在,请求出该点坐标;若不存在,请说明理由.
如图,平面直角坐标系中,一直线l分别交x轴、y轴于点B,C,过点C作直线l的垂线交x轴于点A.若点A的坐标为(2,0)且AC=4,则在直线l上是否存在点P,使△PAB与△BOC相似?若存在,请求出该点坐标;若不存在,请说明理由.
分析 分类讨论:①△PAB∽△OCB,②△PAB∽△COB,①根据勾股定理,可得答案;
②根据相似三角形的性质,可得OB的长,根据待定系数,可得BC的解析式,根据自变量与函数值的对应关系,可得答案.
解答 解:存在点P,使△PAB与△BOC相似,
①当∠B=∠B,∠PAB=∠OCB时,△PAB∽△OCB,如图1 ,
,
由OA=2,AC=4,
解得OC=$\sqrt{A{C}^{2}-O{A}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
即P1(0,2$\sqrt{3}$);
②当∠PAB=∠COB时,△PAB∽△COB,如图2 ,
,
由△OBC∽△OCA,得$\frac{BO}{OC}$=$\frac{OC}{OA}$,
BO=$\frac{O{C}^{2}}{OA}$=$\frac{(2\sqrt{3})^{2}}{2}$=6,
B(-6,0),C(0,2$\sqrt{3}$),设BC的解析式为y=kx+b,
将B、C点坐标代入,得
$\left\{\begin{array}{l}{-6k+b=0}\\{b=2\sqrt{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=2\sqrt{3}}\end{array}\right.$,
BC的解析式为y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$,
当x=2时,y=$\frac{2\sqrt{3}}{3}$+2$\sqrt{3}$=$\frac{8\sqrt{3}}{3}$,
P2(2,$\frac{8\sqrt{3}}{3}$),
综上所述:P1(0,2$\sqrt{3}$),P2(2,$\frac{8\sqrt{3}}{3}$).
点评 本题考查了一次函数综合题,利用相似三角形的性质得出OB的长是解题关键,又利用了待定系数法求函数解析式,自变量与函数值的对应关系,分类讨论是解题关键,以防遗漏.

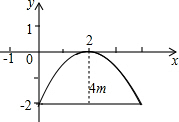 某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.
某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.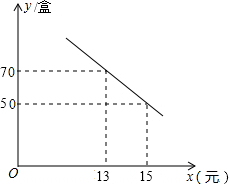 某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示.
某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价x(单位:元)与每日销售量y(单位:盆)之间的函数关系如图所示.