Question

13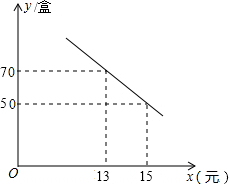．某种鲜花的成本价为每盆12元，在销售中每盆鲜花售价x（单位：元）与每日销售量y（单位：盆）之间的函数关系如图所示．
（1）求y与x的函数关系式．
（2）每盆鲜花的售价定为多少时每日可获得最大利润，最大利润是多少？

Answer 1

分析 （1）利用图象中数据代入一函数解析式，进而得出y与x的关系式；
（2）利用利润=销量×每件利润，进而利用配方法求出函数最值．

解答 解：（1）设y=kx+b，将（13，70），（15，50）代入得：
即$\left\{\begin{array}{l}{13k+b=70}\\{15k+b=50}\end{array}\right.$，
解得：
$\left\{\begin{array}{l}{k=-10}\\{b=200}\end{array}\right.$，
所以y与x之间的函数关系式为：y=-10x+200；
（2）设日销售利润为S，由题意得：
S=（x-12）y
=-10x²+320x-2400
=-10（x-16）²+160，
∴售价为16元/盆时，获最大利润160元．

点评 此题主要考查了二次函数的应用，利用配方法求出函数最值是解题关键．