题目内容
10.化简下列各式的符号,并回答问题:(1)-(-2);(2)+(-$\frac{1}{5}$);(3)-[-(-4)];(4)-[-(+3.5)];(5)-{-[-(-5)]};(6)-{-[-(+5)]}.
问:①当+5前面有2014个负号,化简后结果是多少?
②当-5前面有2015个负号,化简后结果是多少?你能总结出什么规律?
分析 根据相反数的概念进行化简;
①根据相反数的性质进行解答;
②根据相反数的性质解答.
解答 解:(1)-(-2)=2;
(2)+(-$\frac{1}{5}$)=-$\frac{1}{5}$;
(3)-[-(-4)]=-4;
(4)-[-(+3.5)]=+3.5;
(5)-{-[-(-5)]}=5;
(6)-{-[-(+5)]}=-5.
①当+5前面有2014个负号,化简后结果是+5;
②当-5前面有2015个负号,化简后结果是+5,
规律:在一个数的前面有偶数个负号,化简结果是本身;在一个数的前面有奇数个负号,化简结果是这个数的相反数.
点评 本题考查的是相反数的概念,掌握一个数的相反数就是在这个数前面添上“-”号;一个正数的相反数是负数,一个负数的相反数是正数是解题的关键.

练习册系列答案
相关题目
15.设a是任意有理数,下列说法正确的是( )
| A. | (a+1)2的值总是正的 | B. | a2+1的值总是正的 | ||
| C. | -(a+1)2的值总是负的 | D. | a2+1的值中,最大值是1 |
2.在(-2)3,-|-2|,0,-(-9)中,负数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
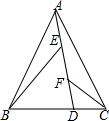 锐角三角形△ABC中,BA=AC,过点A的直线交BC边于点D,E、F是AD上两点,∠BEA=∠AFC且∠BEA与∠AFC都与∠BAC互补,猜想EF、BE、CF之间的关系并证明.
锐角三角形△ABC中,BA=AC,过点A的直线交BC边于点D,E、F是AD上两点,∠BEA=∠AFC且∠BEA与∠AFC都与∠BAC互补,猜想EF、BE、CF之间的关系并证明. 如图,平面直角坐标系中,一直线l分别交x轴、y轴于点B,C,过点C作直线l的垂线交x轴于点A.若点A的坐标为(2,0)且AC=4,则在直线l上是否存在点P,使△PAB与△BOC相似?若存在,请求出该点坐标;若不存在,请说明理由.
如图,平面直角坐标系中,一直线l分别交x轴、y轴于点B,C,过点C作直线l的垂线交x轴于点A.若点A的坐标为(2,0)且AC=4,则在直线l上是否存在点P,使△PAB与△BOC相似?若存在,请求出该点坐标;若不存在,请说明理由. 某园艺公司准备围建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成,已知墙长为20米(如图所示),设垂直于墙的一边长为x米,若所用的篱笆长为32米.
某园艺公司准备围建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成,已知墙长为20米(如图所示),设垂直于墙的一边长为x米,若所用的篱笆长为32米. 如图△ABC中,中线AE、CD相交于G,则S△ABC:S△DEG=12:1.
如图△ABC中,中线AE、CD相交于G,则S△ABC:S△DEG=12:1.