题目内容
3.已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点.若点A的坐标为(-2,0),抛物线的对称轴为直线x=1.则线段AB的长为6.分析 由抛物线y=ax2+bx+c的对称轴为直线x=1,交x轴于A、B两点,其中A点的坐标为(-2,0),根据二次函数的对称性,求得B点的坐标,再求出AB的长度.
解答 解:∵对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,
∴A、B两点关于直线x=1对称,
∵点A的坐标为(-2,0),
∴点B的坐标为(4,0),
AB=4-(-2)=6.
故答案为:6.
点评 此题主要考查了抛物线与x轴的交点的知识,解题的关键是求出B点的坐标,此题难度不大.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
13.杭州跨境贸易产业园(下沙园区)从去年5月7日开园试点到今年1月26日,园区实现进口业务109万单,其中109万用科学记数法表示为( )
| A. | 109×104 | B. | 10.9×105 | C. | 1.09×106 | D. | 0.109×108 |
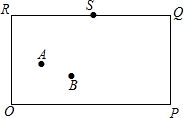 下面设想用电脑模拟台球游戏,为简单起见,约定:
下面设想用电脑模拟台球游戏,为简单起见,约定: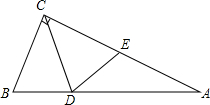 如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
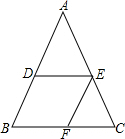 如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.
如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.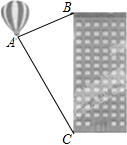 如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.
如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.