题目内容
6.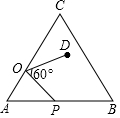 如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )
如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
分析 先计算出OC=6,根据等边三角形的性质得∠A=∠C=60°,再根据旋转的性质得OD=OP,∠POD=60°,根据三角形内角和和平角定义得∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,利用等量代换可得∠2=∠3,然后根据“AAS”判断△AOP≌△CDO,则AP=CO=6.
解答 解:如图,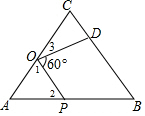
∵AC=9,AO=3,
∴OC=6,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60゜得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,
∴∠1+∠2=120°,∠1+∠3=120°,
∴∠2=∠3,
在△AOP和△CDO中,
∵$\left\{\begin{array}{l}{∠A=∠C}\\{∠2=∠3}\\{OP=OD}\end{array}\right.$,
∴△AOP≌△CDO,
∴AP=CO=6,
故选:C.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质和全等三角形的判定与性质.

练习册系列答案
相关题目
17.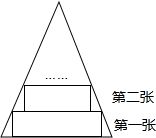 一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )
一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )
 一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )
一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )| A. | 第4张 | B. | 第5张 | C. | 第6张 | D. | 第7张 |
14.我们都有这样的生活经验,要想使多边形(三角形除外)木架不变形至少再钉上若干根木条,如图所示,四边形至少再钉上一根;五边形至少再钉上两根;六边形至少再钉上三根;…,按照此规律,十二边形至少再钉上( )


| A. | 11根 | B. | 10根 | C. | 9根 | D. | 8根 |
18.当x=2时,代数式ax3+bx+1的值为2016,那么x=-2时代数式ax3+bx+1的值为( )
| A. | 2016 | B. | -2015 | C. | -2014 | D. | 2014 |