题目内容
1．观察下列各式：13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
猜想13+23+33+…+93=452．
分析 根据数列可知连续整数的立方和等于这些整数和的平方，据此可得．
解答 解：∵13=12，
13+23=（1+2）2=32，
13+23+33=（1+2+3）2=62，
13+23+33+43=（1+2+3+4）2=102，
∴13+23+33+…+93=（1+2+3+…+9）2=452．
故答案为：452．
点评 本题主要考查数字的变化规律和有理数的混合运算，根据数列得出连续整数的立方和等于这些整数和的平方是解题的关键．
练习册系列答案
相关题目
12．若|x-1|+（y+1）2=0，则x2+y2的值是（ ）
| A． | 0 | B． | 2 | C． | -2 | D． | 1 |
9．把（-8）+（+3）-（-5）-（+7）写成省略括号的代数和形式是（ ）
| A． | -8+3-5-7 | B． | -8-3+8-7 | C． | -8+3+5+7 | D． | -8+3+5-7 |
16．下列单项式中，与a2b是同类项的是（ ）
| A． | ab2 | B． | a2b2 | C． | 3ab | D． | 2a2b |
6．
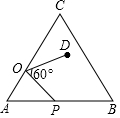如图，在等边△ABC中，AC=9，点O在AC上，且AO=3，点P是AB上一动点，连结OP，将线段OP绕点O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是（ ）
如图，在等边△ABC中，AC=9，点O在AC上，且AO=3，点P是AB上一动点，连结OP，将线段OP绕点O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是（ ）| A． | 3 | B． | 5 | C． | 6 | D． | 8 |
13．某旅游景点三月份共接待游客25万人次，五月份共接待游客64万人次，设每月的平均增长率为x，则可列方程为（ ）
| A． | 25（1+x）2=64 | B． | 25+25（1+x）2=64 | C． | 25（1+2x）=64 | D． | 64（1-x2）=25 |