题目内容
17.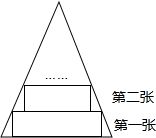 一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )
一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )| A. | 第4张 | B. | 第5张 | C. | 第6张 | D. | 第7张 |
分析 DE为边长为3的正方形的边长,作AH⊥DE于H,交BC于F,如图,BC=15,AF=22.5,DE=3,证明△ADE∽△ABC,则利用相似比可计算出HF=4.5,所以HF=18,由于18÷3=6,原式可判断裁得的纸条中恰为张正方形的纸条是第6张.
解答 解: 如图,BC=15,AF=22.5,DE=3,
如图,BC=15,AF=22.5,DE=3,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AH}{AF}$,即$\frac{3}{15}$=$\frac{AH}{22.5}$,
∴HF=4.5,
∴HF=22.5-4.5=18,
而18÷3=6,
∴裁得的纸条中恰为张正方形的纸条是第6张.
故选C.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,三点应在一条直线上.必须保证在一条直线上,为了使问题简便,尽量构造直角三角形.

练习册系列答案
相关题目
5. 如图,小明在操场上画了一个半径分别为1,2,3的同心圆的图案,现在往这个图案中随机扔一颗石子,这颗石子恰好落在区域C中的概率是( )
如图,小明在操场上画了一个半径分别为1,2,3的同心圆的图案,现在往这个图案中随机扔一颗石子,这颗石子恰好落在区域C中的概率是( )
 如图,小明在操场上画了一个半径分别为1,2,3的同心圆的图案,现在往这个图案中随机扔一颗石子,这颗石子恰好落在区域C中的概率是( )
如图,小明在操场上画了一个半径分别为1,2,3的同心圆的图案,现在往这个图案中随机扔一颗石子,这颗石子恰好落在区域C中的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
12.若|x-1|+(y+1)2=0,则x2+y2的值是( )
| A. | 0 | B. | 2 | C. | -2 | D. | 1 |
2.已知一次函数y=x+b的图象经过第一、二、三象限,则b的值可以是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -1 |
9.把(-8)+(+3)-(-5)-(+7)写成省略括号的代数和形式是( )
| A. | -8+3-5-7 | B. | -8-3+8-7 | C. | -8+3+5+7 | D. | -8+3+5-7 |
6.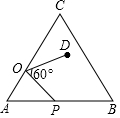 如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )
如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )
 如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )
如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
7.已知A、B是数轴上两点,且点A表示的数是-1.若点B与点A的距离是2,则点B表示的数为( )
| A. | ±2 | B. | -3,1 | C. | -3 | D. | 1 |