题目内容
一组数据的方差为S2,将这组数据中的每一个数据都乘2,再减3,则所得新数据的方差为 .
考点:方差
专题:
分析:设出原来数据的平均数和方差,根据平均数和方差的公式性质求解.
解答:解:设这组数据为x1,x2,…xn,平均数为
,其方差为S12,
将这组数据中的每个数据都乘以2后再减去3,平均数变为2
-3,
则得到的一组新数据的方差为S22=
[(2x1-2
)2+(2x2-2
)2+…+(2xn-2
)2=4S12.
故答案为:4S12.
. |
| x |
将这组数据中的每个数据都乘以2后再减去3,平均数变为2
. |
| x |
则得到的一组新数据的方差为S22=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
故答案为:4S12.
点评:本题考查方差的计算公式的运用:一般地设有n个数据,x1,x2,…xn,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
点P1(x1,y1),点P2(x2,y2)是一次函数y=-2x+4图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
| A、y1>y2 |
| B、y1>y2>0 |
| C、y1<y2 |
| D、y1=y2 |
 已知AD、AE分别为△ABC的角平分线、高线,若∠B=50°,∠C=60°,则∠ADB的度数为( )
已知AD、AE分别为△ABC的角平分线、高线,若∠B=50°,∠C=60°,则∠ADB的度数为( )| A、75° | B、85° |
| C、95° | D、105° |
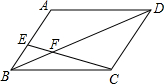 如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则BD=
如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则BD=