题目内容
16.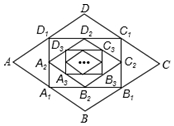 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )| A. | $\frac{5}{{2}^{n-2}}$ | B. | $\frac{5}{{2}^{n-3}}$ | C. | $\frac{5}{{2}^{n}}$ | D. | $\frac{5}{{2}^{n-1}}$ |
分析 根据题意求出菱形ABCD的周长,根据中点四边形的性质得到A2nB2nC2nD2n是菱形,根据题意总结规律得到答案.
解答 解:根据中点四边形的性质可知,A1B1C1D1、A3B3C3D3…是矩形,
A2B2C2D2、A4B4C4D4…是菱形,
∵菱形ABCD的周长是10×4=40,
∴菱形A2B2C2D2的周长是40×$\frac{1}{2}$,
菱形A4B4C4D4的周长是40×$\frac{1}{{2}^{n}}$,
…
则四边形A2nB2nC2nD2n的周长是40×$\frac{1}{{2}^{n}}$=$\frac{5}{{2}^{n-3}}$,
故选:B.
点评 本题考查的是中点四边形的知识,掌握三角形中位线定理和矩形、菱形的判定定理是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.下列说法正确的是( )
| A. | 正负号相反的两个数互为相反数 | |
| B. | 数轴上原点两侧的两个点所表示的数是互为相反数 | |
| C. | 相反数和我们以前学过的倒数是一样的 | |
| D. | 只有正负号不同的两个数称互为相反数,零的相反数是零 |
4.已知线段AB的长为6 cm,点P是线段AB的黄金分割点,则PA的长为(单位:cm)( )
| A. | $3\sqrt{5}-3$ | B. | $9-3\sqrt{5}$或$6-3\sqrt{5}$ | C. | $3\sqrt{5}-3$或$9-3\sqrt{5}$ | D. | $6-3\sqrt{5}$ |
11.下列说法中正确的个数是( )
①不可能事件发生的概率为0;
②“面积相等的两个三角形全等”这一事件是必然事件
③在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值;
④“每次摸一个球,摸到红球的概率是$\frac{1}{6}$”,是指按要求摸6次必有一次摸到的是红球.
①不可能事件发生的概率为0;
②“面积相等的两个三角形全等”这一事件是必然事件
③在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值;
④“每次摸一个球,摸到红球的概率是$\frac{1}{6}$”,是指按要求摸6次必有一次摸到的是红球.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.把多项式(x+1)(x-1)-(1-x)提取公因式(x-1)后,余下的部分是( )
| A. | (x+1) | B. | (x-1) | C. | x | D. | (x+2) |
8.25的平方根是( )
| A. | ±5 | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
5.在2015年“双十一”期间,某网店出售一种电子产品,第一周获得利润2万元,由于产品畅销,利润逐周增加,第3周的利润比第2周的利润增加0.48万元,假设该产品利润每周的增长率相同,则增长率为( )
| A. | 10% | B. | 15% | C. | 20% | D. | 120% |
6.在函数y=$\frac{-{a}^{2}-1}{x}$(a为常数)的图象上有三点A(-3,y1),B(-1,y2),C(3,y3),则函数值y1、y2、y3的大小关系是( )
| A. | y2<y3<y1 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y3<y1<y2 |