题目内容
11.下列说法中正确的个数是( )①不可能事件发生的概率为0;
②“面积相等的两个三角形全等”这一事件是必然事件
③在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值;
④“每次摸一个球,摸到红球的概率是$\frac{1}{6}$”,是指按要求摸6次必有一次摸到的是红球.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据概率的意义判断即可.
解答 解:①不可能事件发生的概率为0,此结论正确;
②“面积相等的两个三角形全等”这一事件是随机事件,此结论错误;
③在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值,此结论正确;
④“每次摸一个球,摸到红球的概率是$\frac{1}{6}$”,是指按要求摸6次可能有一次摸到的是红球,此结论错误;
故选:B.
点评 本题主要考查概率的意义,熟练掌握概率的定义及频率估计概率的意义是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
1. 如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )
如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )
 如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )
如图,AB∥CD,CE平分∠BCD,∠DCE=20°,则∠B的度数为( )| A. | 18° | B. | 40° | C. | 45° | D. | 54° |
19.下列表述正确的是( )
| A. | -(-10)<0 | B. | (-10)2<92 | C. | -102<0 | D. | -(-10)2>0 |
6. 如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为( )
如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为( )
 如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为( )
如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为( )| A. | 9 | B. | 6 | C. | 4 | D. | 3 |
16.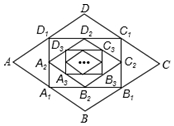 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )| A. | $\frac{5}{{2}^{n-2}}$ | B. | $\frac{5}{{2}^{n-3}}$ | C. | $\frac{5}{{2}^{n}}$ | D. | $\frac{5}{{2}^{n-1}}$ |
3.设$\sqrt{2}$=a,$\sqrt{3}$=b,用含a,b的式子表示$\sqrt{6}$,则下列表示正确的是( )
| A. | ab2 | B. | 2ab | C. | ab | D. | a2b |
20.下列各组中的两项是同类项的是( )
| A. | -m2n和-mn2 | B. | 0.5a和0.5b | C. | 320和4×105 | D. | -m2和3m |