题目内容
7.小马虎在计算一个多项式减去2a2+a-5的差时,因一时疏忽忘了对两个多项式用括号括起来,因此减去后面两项没有变号,结果得到的差是a2+3a-1.(1)求这个多项式;
(2)算出此题的正确的结果.
分析 (1)根据题意可以求得相应的多项式;
(2)根据(1)中的结果可以求得正确的结果.
解答 解:(1)由题意可得,
这个多项式是:a2+3a-1+2a2-a+5=3a2+2a+4,
即这个多项式是3a2+2a+4;
(2)由(1)可得,
3a2+2a+4-(2a2+a-5)
=3a2+2a+4-2a2-a+5
=a2+a+9,
即此题的正确的结果是a2+a+9.
点评 本题考查整式的加减,解答本题的关键是明确整式的加减的计算方法,求出相应的多项式.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
18.在-2,0,3,π这四个数中,最大的数是( )
| A. | -2 | B. | 0 | C. | 3 | D. | π |
15.已知单项式-5am-1b6与$\frac{1}{2}$ab2n的和仍是单项式,则m-n的值是( )
| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
12.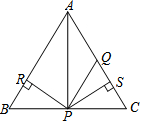 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )| A. | ①②③④ | B. | ②③④ | C. | ①③④⑤ | D. | ①②③⑤ |
19.下列表述正确的是( )
| A. | -(-10)<0 | B. | (-10)2<92 | C. | -102<0 | D. | -(-10)2>0 |
16.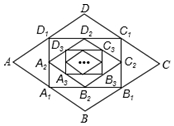 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A2nB2nC2nD2n的周长是( )| A. | $\frac{5}{{2}^{n-2}}$ | B. | $\frac{5}{{2}^{n-3}}$ | C. | $\frac{5}{{2}^{n}}$ | D. | $\frac{5}{{2}^{n-1}}$ |
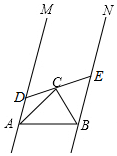 已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E.若AB=10,AD=4,则BE=6.
已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E.若AB=10,AD=4,则BE=6.