题目内容
11.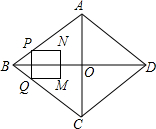 如图,在菱形ABCD中,AB=5cm,AC=6cm,对角线AC、BD相交于点O.动点P从点B出发,沿折线BA-AD以1cm/s的速度向终点D运动,过点P作PQ∥AC交折线BC-CD于点Q,以PQ为边作正方形PQMN,且MN与AC始终在PQ的同侧.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,在菱形ABCD中,AB=5cm,AC=6cm,对角线AC、BD相交于点O.动点P从点B出发,沿折线BA-AD以1cm/s的速度向终点D运动,过点P作PQ∥AC交折线BC-CD于点Q,以PQ为边作正方形PQMN,且MN与AC始终在PQ的同侧.设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s).(1)求点P在AB边上时PQ的长度(用含t的代数式表示).
(2)当点N落在AC上时,求t的值.
(3)当点P在AB边上时,求S与t之间的函数关系式.
(4)当正方形PQMN与菱形ABCD重叠部分图形是六边形时,直接写出t的取值范围.
分析 (1)根据△BPQ∽△BAC,对应边成比例得出$\frac{PQ}{AC}$=$\frac{BP}{BA}$,即$\frac{PQ}{6}$=$\frac{t}{5}$,即可求得PQ=$\frac{6}{5}$t.
(2)根据勾股定理求得OB,然后分两种情况分别讨论即可求得;
(3)分两种情况,根据图形求得即可;
(4)分别求得当P、Q、M、N四点都在菱形四条边上时和MN经过D点和B点时的t的值,即可求得正方形PQMN与菱形ABCD重叠部分图形是六边形时t的取值范围.
解答 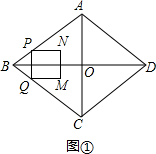 解:(1)如图①,
解:(1)如图①,
∵PQ∥AC,
∴△BPQ∽△BAC.
∴$\frac{PQ}{AC}$=$\frac{BP}{BA}$.即$\frac{PQ}{6}$=$\frac{t}{5}$.
∴PQ=$\frac{6}{5}$t.
(2)∵四边形ABCD是菱形,
∴AC⊥BD.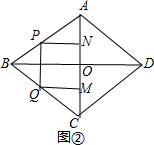 ∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=4.
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=4.
①如图②,当0<t≤5时,
∵cos∠APN=cos∠ABO,
∴$\frac{PN}{PA}$=$\frac{BO}{AB}$=$\frac{4}{5}$,即$\frac{5-t}{5}$=$\frac{\frac{6}{5}t}{4}$,
∴t=2.
②如图③,当5<t≤10时,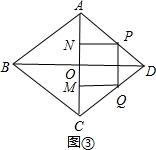 PQ=$\frac{6}{5}$(10-t).
PQ=$\frac{6}{5}$(10-t).
∵cos∠APN=cos∠ADO,
∴$\frac{PN}{PA}$=$\frac{DO}{AD}$=$\frac{4}{5}$,即$\frac{\frac{6}{5}(10-t)}{t-5}$=$\frac{4}{5}$
∴t=8.
(3)①如图①,当0<t≤2时,S=PQ2=($\frac{6}{5}$t)2=$\frac{36}{25}$t2.
②如图④,当2<t<5时,设PN、QM与AC分别交于点G、H.则PG=$\frac{4}{5}$(5-t).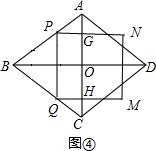 ∴S=PQ•PG=$\frac{6}{5}$t•$\frac{4}{5}$(5-t)=-$\frac{24}{25}$t2+$\frac{24}{5}$t.
∴S=PQ•PG=$\frac{6}{5}$t•$\frac{4}{5}$(5-t)=-$\frac{24}{25}$t2+$\frac{24}{5}$t.
(4)如图⑤,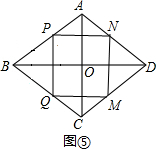
当P、Q、M、N四点都在菱形四条边上时,则$\frac{PN}{BD}$=$\frac{PA}{AB}$,即$\frac{\frac{6}{5}t}{8}$=$\frac{5-t}{5}$,
∴t=$\frac{20}{7}$,
如图⑥,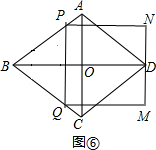
当MN经过D点时,则(8-$\frac{6}{5}$t)2+($\frac{3}{5}$t)2=t2,
∴t=4;
∴当正方形PQMN与菱形ABCD重叠部分图形是六边形时,$\frac{20}{7}$<t<4或6<t<$\frac{50}{7}$.
点评 本题是四边形的综合题,考查了菱形的性质,正方形的性质,三角形相似的判定和性质,分类讨论思想的运用和数形结合思想的运用是解题的关键.

| A. | 了解一批炮弹的杀伤半径 | B. | 了解三明市每天的流动人口数 | ||
| C. | 对“神舟8号”载入飞船的零件检查 | D. | 要了解三明市居民日平均用水量 |
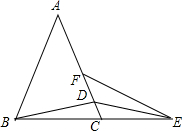 如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.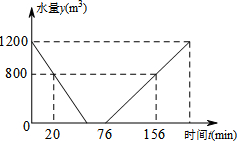 江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式
江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式 如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.