题目内容
12. 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
分析 先根据AB⊥OC′,OS⊥OC′可知△ABC∽△SOC,同理可得△A′B′C′∽△SOC′,再由相似三角形的对应边成比例即可得出h的值.
解答 解:∵AB⊥OC′,OS⊥OC′,
∴SO∥AB,
∴△ABC∽△SOC,
∴$\frac{BC}{BC+OB}$=$\frac{AB}{OS}$,即$\frac{1}{1+OB}$=$\frac{1.5}{h}$,
同理,∵A′B′⊥OC′,
∴△A′B′C′∽△SOC′,
∴$\frac{B′C′}{B′C′+BB′+OB}$=$\frac{A′B′}{OS}$,
即$\frac{1.8}{1.8+3.2+OB}$=$\frac{1.5}{h}$②,
故$\frac{1.8}{5+OB}$=$\frac{1}{1+OB}$,
解得:OB=4,
则$\frac{1}{5}$=$\frac{1.5}{h}$,
解得:h=7.5,
答:路灯离地面的高度是7.5米.
点评 本题考查的是相似三角形在实际生活中的应用,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象与正比例函数的图象交于A,B两点,且点A在第二象限,点A的横坐标为-1,过点A作AC⊥x轴,垂足为C,△ACB的面积为2.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象与正比例函数的图象交于A,B两点,且点A在第二象限,点A的横坐标为-1,过点A作AC⊥x轴,垂足为C,△ACB的面积为2.
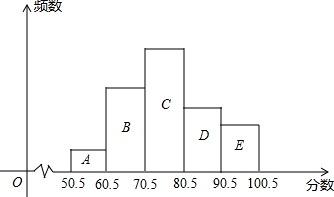 从某校参加科普知识竞赛的学生试卷中,抽取一个样本了解竞赛成绩的分布情况,将样本分成A、B、C、D、E五个组,绘制成如图所示的频数分布直方图,图中A、B、C、D、E各小组的长方形的高的比是l:4:6:3:2,且A组的频数是5,请结合直方图提供的信息,解答下列问题.
从某校参加科普知识竞赛的学生试卷中,抽取一个样本了解竞赛成绩的分布情况,将样本分成A、B、C、D、E五个组,绘制成如图所示的频数分布直方图,图中A、B、C、D、E各小组的长方形的高的比是l:4:6:3:2,且A组的频数是5,请结合直方图提供的信息,解答下列问题. 如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx+b的图象交于点A(m,2),设一次函数y=kx+b的图象与y轴交于点B,且△AOB的面积为3
如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx+b的图象交于点A(m,2),设一次函数y=kx+b的图象与y轴交于点B,且△AOB的面积为3