题目内容
6.已知,矩形ABCD中,AB=2,BC=4,将矩形ABCD折叠,使点C落在直线AB上的点P处,折痕与边AD、BC分别交于E、F.若AP=1,则折痕EF的长为$\frac{\sqrt{17}}{2}$.分析 如图,作辅助线;首先证明PE=CE,PF=CF;设DE=λ,则AE=4-λ,运用勾股定理列出关于λ的方程,求出λ;同理可求CF;进而求出QF;运用勾股定理求出EF,即可解决问题.
解答 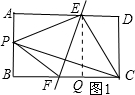 解:如图1,过点E作EQ⊥BC于点M;
解:如图1,过点E作EQ⊥BC于点M;
∵四边形ABCD为矩形,
∴AD=BC=4,DC=AB=2;
由题意得:PE=CE,PF=CF;PA=PB=1;
设DE=λ,则AE=4-λ,
由勾股定理得:
CD2+DE2=AE2+AP2=PE2,
即22+λ2=(4-λ)2+12,
解得:λ=$\frac{13}{8}$;同理可求CF=$\frac{17}{8}$,
∴QF=$\frac{17}{8}-\frac{13}{8}$=$\frac{1}{2}$;而EQ=CD=2,
∴由勾股定理得:EF2=EQ2+FQ2,
解得:EF=$\frac{\sqrt{17}}{2}$,
故答案为$\frac{\sqrt{17}}{2}$.
点评 该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用翻折变换的性质等知识点来分析、判断、解答.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
6.在四边形ABCD中,若∠A:∠B:∠C:∠D=5:m:4:n,则( )
| A. | m+n=9 | B. | 4m=5n | C. | 5m=4n | D. | 以上都不对 |
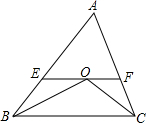 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E.交AC于F,若BE=3,CF=2,则EF的长为5.
 如图所示,点A在点O的北偏东50°方向,点B在点O的南偏东10°方向上,则∠AOB=120°.
如图所示,点A在点O的北偏东50°方向,点B在点O的南偏东10°方向上,则∠AOB=120°. 如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°.
如图,小敏从A处出发沿南偏东65°方向行走至B处,又沿北偏西15°方向行走至C处,则∠ABC的度数是50°. 如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于6cm.
如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于6cm.