题目内容
18.已知实数x、y、z满足$\frac{x}{y+z}$+$\frac{y}{z+x}$+$\frac{z}{x+y}$=1,则$\frac{{x}^{2}}{y+z}$+$\frac{{y}^{2}}{z+x}$+$\frac{{z}^{2}}{x+y}$的值是( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 利用$\frac{x}{y+z}$+$\frac{y}{z+x}$+$\frac{z}{x+y}$=1分别乘x,y,z再相加求解即可.
解答 解:∵$\frac{x}{y+z}$+$\frac{y}{z+x}$+$\frac{z}{x+y}$=1,
∴$\frac{{x}^{2}}{y+z}$+$\frac{yx}{z+x}$+$\frac{zx}{x+y}$=x,$\frac{xy}{y+z}$+$\frac{{y}^{2}}{z+x}$+$\frac{zy}{x+y}$=y,$\frac{xz}{y+z}$+$\frac{yz}{z+x}$+$\frac{{z}^{2}}{x+y}$=z,
∴$\frac{{x}^{2}}{y+z}$+$\frac{{y}^{2}}{z+x}$+$\frac{{z}^{2}}{x+y}$+($\frac{yx}{z+x}$+$\frac{yz}{z+x}$)+($\frac{zx}{x+y}$+$\frac{zy}{x+y}$)+($\frac{xy}{y+z}$+$\frac{xz}{y+z}$)=x+y+z,
∴$\frac{{x}^{2}}{y+z}$+$\frac{{y}^{2}}{z+x}$+$\frac{{z}^{2}}{x+y}$+y+z+x=x+y+z,
∴$\frac{{x}^{2}}{y+z}$+$\frac{{y}^{2}}{z+x}$+$\frac{{z}^{2}}{x+y}$=0.
故选:B.
点评 本题主要考查了分式的化简求值,解题的关键是利用$\frac{x}{y+z}$+$\frac{y}{z+x}$+$\frac{z}{x+y}$=1,列出$\frac{{x}^{2}}{y+z}$+$\frac{{y}^{2}}{z+x}$+$\frac{{z}^{2}}{x+y}$的式子.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
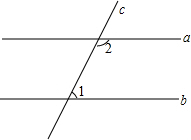 如图,直线a,b被直线c所截,且a∥b,∠1=40°,则∠2=140度.
如图,直线a,b被直线c所截,且a∥b,∠1=40°,则∠2=140度.