题目内容
2.已知,如图1,AD∥BC,∠A=∠BCD,点E是射线BC上一动点,试回答下列问题:(1)求证:AB∥CD;
(2)如图2,若点E在B、C两点之间时,DM平分∠ADE,DN平分∠CDE,试探索∠NDN与∠B的数量关系,并说明理由;
(3)在(2)的条件下.点E在点C右侧时,(2)中的结论是否仍成立?若成立,请说明理由:若不成立,求∠MDN与∠B的比值.
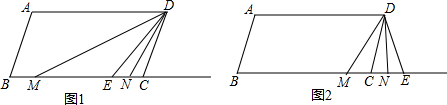
分析 (1)由AD∥BC得∠A+∠B=180°,根据∠A=∠BCD知∠BCD+∠B=180°,得证;
(2)根据AD∥BC、AB∥CD得∠ADC=∠B,由角平分线知∠MDE=$\frac{1}{2}$∠ADE、∠NDE=$\frac{1}{2}$∠EDC,将∠MDE+∠NDE可得;
(3)根据AD∥BC、AB∥CD得∠ADC=∠B,由角平分线知∠MDE=$\frac{1}{2}$∠ADE、∠NDE=$\frac{1}{2}$∠EDC,将∠MDE-∠NDE可得.
解答 解:(1)∵AD∥BC,
∴∠A+∠B=180°,
又∵∠A=∠BCD,
∴∠BCD+∠B=180°,
∴AB∥CD;
(2)∠MDN=$\frac{1}{2}$∠B,
∵AD∥BC,
∴∠BCD+∠ADC=180°,
又∵∠BCD+∠B=180°,
∴∠ADC=∠B,
∵DM平分∠ADE,DN平分∠EDC,
∴∠MDE=$\frac{1}{2}$∠ADE,∠NDE=$\frac{1}{2}$∠EDC,
∴∠MDE+∠NDE=$\frac{1}{2}$∠ADC,
即∠MDN=$\frac{1}{2}$∠B;
(3)仍然成立,
∵AD∥BC,
∴∠BCD+∠ADC=180°,
又∵∠BCD+∠B=180°,
∴∠ADC=∠B,
∵DM平分∠ADE,DN平分∠EDC,
∴∠MDE=$\frac{1}{2}$∠ADE,∠NDE=$\frac{1}{2}$∠EDC,
∴∠MDE-∠NDE=$\frac{1}{2}$∠ADC,
即∠MDN=$\frac{1}{2}$∠B.
点评 本题主要考查了平行线的判定与性质、角平分线的性质,熟练掌握平行线的判定与性质是基础,将待求角度转化成其他角的和、差是解题关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 不相交的两条线段是平行线 | |
| B. | 不相交的两条直线是平行线 | |
| C. | 不相交的两条射线是平行线 | |
| D. | 在同一平面内,不相交的两条直线是平行线 |
17.如图中,∠1与∠2是对顶角的是( )
| A. |  | B. | 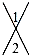 | C. | 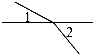 | D. | 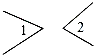 |
14.若5a=2b=10,则$\frac{1}{a}$+$\frac{1}{b}$的值为( )
| A. | 10 | B. | $\frac{1}{10}$ | C. | 1 | D. | $\frac{7}{10}$ |
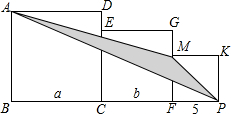 如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.
如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.