题目内容
12.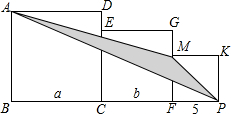 如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.
如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.(1)求阴影部分面积;(结果用含字母的代数式表示)
(2)当a=5$\sqrt{3}$厘米,b=4$\sqrt{3}$厘米时,求阴影部分面积.
分析 (1)由AC∥PM,得S△APM=S△CPM,由此即可解决问题.
(2)代入(1)中结论即可.
解答 解:(1)如图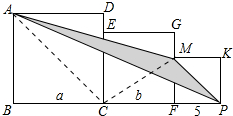 连接AC、CM.
连接AC、CM.
∵四边形ABCD,MFPK是正方形,
∴∠ACB=∠MPF=45°,
∴AC∥MP,
∴S△APM=S△CPM=$\frac{1}{2}$•CP•MF=$\frac{1}{2}$(b+5)•5=$\frac{25}{2}$+$\frac{5b}{2}$.
(2)当b=4$\sqrt{3}$时,S△APM=$\frac{25}{2}$+10$\sqrt{3}$.
点评 本题考查正方形的性质、整式的混合运算等知识,解题的关键是把△APM的面积转化为△CPM的面积,记住同底等高的三角形面积相等,属于中考常考题型.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
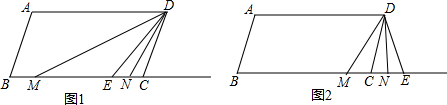
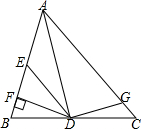 AD为∠BAC平分线,DF⊥AB,DE=DG,S△ADG=50,S△ADE=39,求S△EDF.
AD为∠BAC平分线,DF⊥AB,DE=DG,S△ADG=50,S△ADE=39,求S△EDF.