若5a=2b=10.则$\frac{1}{a}$+$\frac{1}{b}$的值为( )A．10B．$\frac{1}{10}$C．1D．$\frac{7}{10}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．若5^a=2^b=10，则$\frac{1}{a}$+$\frac{1}{b}$的值为（　　）

A．

B．

$\frac{1}{10}$

C．

D．

$\frac{7}{10}$

分析根据幂的乘方进行计算解答即可．

解答解：∵（5^a）^b=5^ab=10^b，（2^b）^a=2^ab=10^a，
∴5^ab•2^ab=10^a•10^b，
即10^ab=10^a+b，
可得：ab=a+b，
$\frac{1}{a}+\frac{1}{b}=1$．
故选C．

点评此题考查幂的乘方问题，关键是根据幂的乘方的逆运算解答．

练习册系列答案

相关题目

4．$\sqrt{100}$的结果是（　　）

${x^2}-x+\frac{1}{4}$

B．

x²-xy+y²

C．

$\frac{1}{4}{m^2}+9{n^2}$

D．

x⁶-10x³-25

2．已知，如图1，AD∥BC，∠A=∠BCD，点E是射线BC上一动点，试回答下列问题：
（1）求证：AB∥CD；
（2）如图2，若点E在B、C两点之间时，DM平分∠ADE，DN平分∠CDE，试探索∠NDN与∠B的数量关系，并说明理由；
（3）在（2）的条件下．点E在点C右侧时，（2）中的结论是否仍成立？若成立，请说明理由：若不成立，求∠MDN与∠B的比值．

9．观察下列等式：
①$\sqrt{1-\frac{1}{2}}=\sqrt{\frac{1}{2}}$；②$\sqrt{2-\frac{2}{5}}=2\sqrt{\frac{2}{5}}$；③$\sqrt{3-\frac{3}{10}}=3\sqrt{\frac{3}{10}}$；④$\sqrt{4-\frac{4}{17}}=4\sqrt{\frac{4}{17}}$；…
（1）试猜想第⑤个等式应为$\sqrt{5-\frac{5}{26}}=5\sqrt{\frac{5}{26}}$；
（2）试用含n（n为正整数）的式子表示你发现的规律．

19．某校积极推进“阳光体育活动”，本学期在九年级11个班中开展篮球单循环比赛（每个班与其他班级分别进行一场比赛，每班共要进行10场比赛），比赛规则规定每场比赛都要分出胜负，胜一场得3分，负一场得-1分，赛后有A，B，C，D四个班级得分情况如下表：

参加班级	A	B	C	D
得分情况	14	18	10	6

（1）根据以上信息，求A，B，C，D四个班级的平均分；
（2）若A班在所有的比赛中总得分为14分，则该班胜了几场？
（3）假设比赛结束后，E班得分比F，C两班得分之和的2倍还多2分，且E班获胜场数超过F，G两班获胜场数之和，请求出E班胜了几场？

6．小丽同学解方程8x²-x-2=0的简要步骤如下：
解：8x²-x-2=0，
两边同除以8第一步：x²-$\frac{1}{8}$x-$\frac{1}{4}$=0．
移项第二步：x²-$\frac{1}{8}$x=$\frac{1}{4}$，
配方第三步：（x-$\frac{1}{12}$）²=$\frac{1}{4}$$+\frac{1}{12}$，
开平方第四步：x-$\frac{1}{12}$=±$\sqrt{\frac{1}{3}}$，
移项第五步：x₁=$\frac{1}{12}$+$\sqrt{\frac{1}{2}}$，x₂=$\frac{1}{12}$-$\sqrt{\frac{1}{2}}$，
上述过程，发生第一次错误是在第三步，改正这一步．

3．

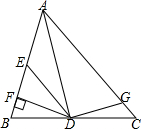AD为∠BAC平分线，DF⊥AB，DE=DG，S_△ADG=50，S_△ADE=39，求S_△EDF．

1．探究
问题1  已知：如图1，三角形ABC中，点D是AB边的中点，AE⊥BC，BF⊥AC，垂足分别为点E，F，AE，BF交于点M，连接DE，DF．若DE=kDF，则k的值为1．
拓展
问题2  已知：如图2，三角形ABC中，CB=CA，点D是AB边的中点，点M在三角形ABC的内部，且∠MAC=∠MBC，过点M分别作ME⊥BC，MF⊥AC，垂足分别为点E，F，连接DE，DF．求证：DE=DF．
推广
问题3  如图3，若将上面问题2中的条件“CB=CA”变为“CB≠CA”，其他条件不变，试探究DE与DF之间的数量关系，并证明你的结论．

试题分类