题目内容
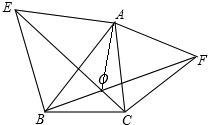 如图,已知△ABC,分别以AB、AC为边作等边△ABE和等边△ACF,BF、CE交于点O.求证:
如图,已知△ABC,分别以AB、AC为边作等边△ABE和等边△ACF,BF、CE交于点O.求证:(1)BF=CE;
(2)∠BOE=60°;
(3)AO平分∠EOF;
(4)∠BEC+∠BFC=∠BAC.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:(1)由条件证明△AEC≌△ABF即可得出结论;
(2)由(1)可得∠AEC=∠ABF,且∠AEC+∠EAB=∠ABF+∠BOF,可得出结论;
(3)过A分别作AM⊥EC,AN⊥BF,证明△AEM≌△ABN,可得出AM=AN,可得出结论;
(4)由(3)可知∠AOF=∠AOE=60°,∠BEC+∠EBA=∠BAO+∠AOE,可得出∠BEC=∠BAO,同理可得∠BFC=∠CAO,相加可得出结论.
(2)由(1)可得∠AEC=∠ABF,且∠AEC+∠EAB=∠ABF+∠BOF,可得出结论;
(3)过A分别作AM⊥EC,AN⊥BF,证明△AEM≌△ABN,可得出AM=AN,可得出结论;
(4)由(3)可知∠AOF=∠AOE=60°,∠BEC+∠EBA=∠BAO+∠AOE,可得出∠BEC=∠BAO,同理可得∠BFC=∠CAO,相加可得出结论.
解答:证明:(1)∵△ABE和△ACF为等边三角形,
∴AE=AB,AC=AF,∠EAB=∠FAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中,
,
∴△AEC≌△ABF(SAS),
∴BF=CE;
(2)由(1)△AEC≌△ABF,
∴∠AEC=∠ABF,
∵∠AEC+∠EAB=∠ABF+∠BOE,
∴∠BOE=∠EAB=60°;
(3)如图,过A分别作AM⊥EC,AN⊥BF,分别交EC、BF于点M、N
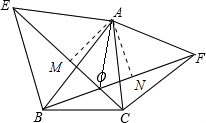
由(1)可得∠AEM=∠ABN,
在△AEM和△ABN中,
,
∴△AEM≌△ABN(AAS),
∴AM=AN,
∴点A在∠EOF的角平分线上,
∴AO平分∠EOF;
(4)由(3)可知∠AOE=∠EBA=60°,
且∠BEC+∠EBA=∠BAO+∠AOE,
∴∠BEC=∠BAO,
同理∠BFC=∠CAO,
∴∠BEC+∠BFC=∠BAO+∠CAO=∠BAC.
∴AE=AB,AC=AF,∠EAB=∠FAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中,
|
∴△AEC≌△ABF(SAS),
∴BF=CE;
(2)由(1)△AEC≌△ABF,
∴∠AEC=∠ABF,
∵∠AEC+∠EAB=∠ABF+∠BOE,
∴∠BOE=∠EAB=60°;
(3)如图,过A分别作AM⊥EC,AN⊥BF,分别交EC、BF于点M、N

由(1)可得∠AEM=∠ABN,
在△AEM和△ABN中,
|
∴△AEM≌△ABN(AAS),
∴AM=AN,
∴点A在∠EOF的角平分线上,
∴AO平分∠EOF;
(4)由(3)可知∠AOE=∠EBA=60°,
且∠BEC+∠EBA=∠BAO+∠AOE,
∴∠BEC=∠BAO,
同理∠BFC=∠CAO,
∴∠BEC+∠BFC=∠BAO+∠CAO=∠BAC.
点评:本题主要考查全等三角形的判定和性质及等边三角形的、三角形内角和定理的综合应用,熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
 如图A、B、C、D在同一直线上,BE⊥AD,CF⊥AD,垂足分别是B,C,AB=DC,AE=DF.求证:AF=DE.
如图A、B、C、D在同一直线上,BE⊥AD,CF⊥AD,垂足分别是B,C,AB=DC,AE=DF.求证:AF=DE.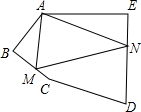 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在边BC、DE上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM=
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在边BC、DE上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM=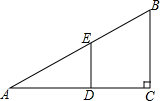 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,D、E分别为AC和AB上的一个动点,则BD+DE的最小值是 如图,在正方形ABCD中,E为AD中点,G为DC上一点,且DG=
如图,在正方形ABCD中,E为AD中点,G为DC上一点,且DG=