题目内容
7.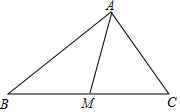 如图,在△ABC中,AM是BC边上的中线,求证:AM<(AB+AC).
如图,在△ABC中,AM是BC边上的中线,求证:AM<(AB+AC).
分析 延长AM到D,使MD=AM,连CD,证△ABM≌△DCM得AB=CD,进而在△ACD中利用三角形三边关系,证之.
解答 证明:如图,延长AM到D,使MD=AM,连CD,
∵AM是BC边上的中线,
∴BM=CM,
在△ABM和△DCM中,
∵$\left\{\begin{array}{l}{BM=CM}\\{∠BMA=∠CMD}\\{AM=DM}\end{array}\right.$,
∴△ABM≌△DCM(SAS),
∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
∴AM<$\frac{1}{2}$(AB+AC)<AB+AC.
点评 本题主要考查了全等三角形的判定及性质以及三角形的三边关系问题,添加辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目

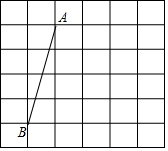 如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.
如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上. 已知等腰三角形的周长为6cm,底边长y(cm)是腰长x(cm)的函数,
已知等腰三角形的周长为6cm,底边长y(cm)是腰长x(cm)的函数,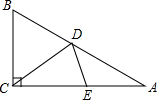 如图,Rt△ABC中,∠ACB=90°,∠B=60°,AB=2,点D是边AB上任意一点,点E是边AC上任意一点,连接DE、DE,则DC+DE的最小值为$\frac{3}{2}$.
如图,Rt△ABC中,∠ACB=90°,∠B=60°,AB=2,点D是边AB上任意一点,点E是边AC上任意一点,连接DE、DE,则DC+DE的最小值为$\frac{3}{2}$.