题目内容
2.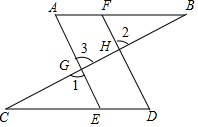 请把以下证明过程补充完整,并在下面的括号内填上推理理由:
请把以下证明过程补充完整,并在下面的括号内填上推理理由:已知:如图,∠1=∠2,∠A=∠D.
求证:∠B=∠C
证明:∵∠1=∠2,(已知)
又:∵∠1=∠3,对顶角相等
∴∠2=∠3,(等量代换)
∴AE∥FD同位角相等,两直线平行
∴∠A=∠BFD两直线平行,同位角相等
∵∠A=∠D(已知)
∴∠D=∠BFD(等量代换)
∴AB∥CD内错角相等,两直线平行
∴∠B=∠C两直线平行,内错角相等.
分析 先根据题意得出∠2=∠3,故可得出AE∥FD,故∠A=∠BFD,再由∠A=∠D可得出∠D=∠BFD,
故可得出AB∥CD,进而可得出结论.
解答 证明:∵∠1=∠2(已知),
又∵∠1=∠3对顶角相等,
∴∠2=∠3(等量代换),
∴AE∥FD (同位角相等,两直线平行),
∴∠A=∠BFD (两直线平行,同位角相等).
∵∠A=∠D(已知),
∴∠D=∠BFD(等量代换),
∴AB∥CD (内错角相等,两直线平行).
∴∠B=∠C (两直线平行,内错角相).
故答案为:对顶角相等;∠3;同位角相等,两直线平行;两直线平行,同位角相等;∠BFD;AB,内错角相等,两直线平行;两直线平行,内错角相等.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
12.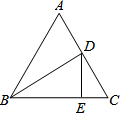 如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=1.5,则AB的长为( )
如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=1.5,则AB的长为( )
 如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=1.5,则AB的长为( )
如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC于点E,且CE=1.5,则AB的长为( )| A. | 3 | B. | 4.5 | C. | 6 | D. | 7.5 |
10. 如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.
如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.
 如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.
如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.| A. | $\frac{1500}{sinα}$ | B. | 1500sinα | C. | 1500cosα | D. | $\frac{1500}{tanα}$ |
14. 如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )
如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )
 如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )
如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是( )| A. | 0 | B. | 7 | C. | 快 | D. | 乐 |
12.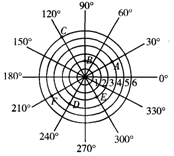 如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
 如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )| A. | A(4,30°) | B. | B(2,90°) | C. | C(6,120°) | D. | D(3,240°) |
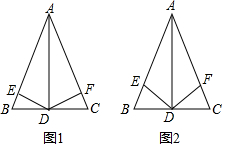 (1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.