题目内容
13.若$\sqrt{{x}^{2}-6x+9}$=3-x,则化简$\sqrt{{x}^{2}-10x+25}$-$\sqrt{{x}^{2}-14x+49}$=-2.分析 根据二次根式的性质,可得x≤3,根据二次根式的性质,可化简二次根式,根据整式的加减,可得答案.
解答 解:由$\sqrt{{x}^{2}-6x+9}$=3-x,得
x≤3.
$\sqrt{{x}^{2}-10x+25}$-$\sqrt{{x}^{2}-14x+49}$=5-x-(7-x)=-2,
故答案为:-2.
点评 本题考查了二次根式的加减,利用二次根式的性质化简二次根式是解题关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
3.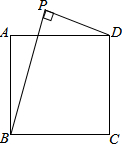 如图,在正方形ABCD中,CD=$\sqrt{2}$,若在线段AD上方有一点P,满足PD=1,且∠BPD=90°,则点A到BP的距离为( )
如图,在正方形ABCD中,CD=$\sqrt{2}$,若在线段AD上方有一点P,满足PD=1,且∠BPD=90°,则点A到BP的距离为( )
 如图,在正方形ABCD中,CD=$\sqrt{2}$,若在线段AD上方有一点P,满足PD=1,且∠BPD=90°,则点A到BP的距离为( )
如图,在正方形ABCD中,CD=$\sqrt{2}$,若在线段AD上方有一点P,满足PD=1,且∠BPD=90°,则点A到BP的距离为( )| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | ||
| C. | $\frac{\sqrt{3}}{2}$ | D. | 条件不足,无法计算 |
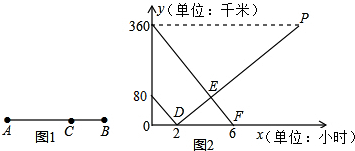
5. 如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
 如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )
如图,已知a∥b,且∠2是∠1的2倍,那么∠2的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
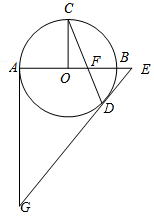 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F.过点D作⊙O的切线交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F.过点D作⊙O的切线交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.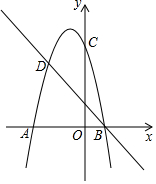 已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).
已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).