题目内容
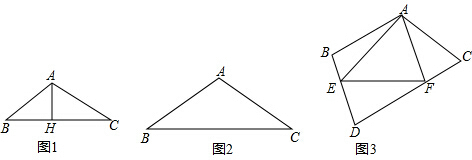
20．
如图，在△ABC中，锐角∠C=θ°，BC=a，AC=b．（1）试说明S△ABC=$\frac{1}{2}$ab•sinθ；
（2）若a=3，b=4，θ=45°，则S△ABC=3$\sqrt{2}$．
分析 （1）过B作BD与AC垂直，在直角三角形BCD中，利用锐角三角函数定义表示出BD，根据三角形面积公式验证即可；
（2）将各自的值代入（1）结果中计算即可求出面积．
解答 
（1）证明：过B作BD⊥AC，
在Rt△BCD中，∠C=θ°，BC=a，
∴BD=asinθ，
则S△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$ab•sinθ；
（2）解：∵a=3，b=4，θ=45°，
∴S△ABC=$\frac{1}{2}$ab•sinθ=3$\sqrt{2}$，
故答案为：3$\sqrt{2}$
点评 此题考查了解直角三角形，熟练掌握锐角三角函数定义是解本题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
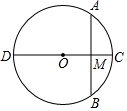如图，⊙O的直径为CD，AB是⊙O的弦，AB⊥CD，垂足为M，AB=10，MD=5MC，则⊙O半径的长是3$\sqrt{5}$．
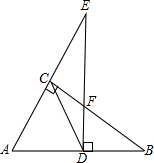已知：如图所示，CD是直角△ABC的斜边中线，过点D垂直于AB的直线交BC于点F，交AC的延长线于点E，求证：CD2=DF•DE．
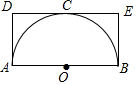如图，AB是半圆O的直径，过半圆O上一点C的切线与过A，B两点的两条直线分别垂直相交于点D，E，若点C是劣弧$\widehat{AB}$的中点，求证：四边形ABED是矩形．
如图所示，线段AB长为a，点C是AB的中点，点D在AB上，若CD=b（b＜$\frac{a}{2}$），则线段AD的长为$\frac{1}{2}$a-b或$\frac{1}{2}$a+b．