题目内容
11.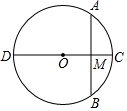 如图,⊙O的直径为CD,AB是⊙O的弦,AB⊥CD,垂足为M,AB=10,MD=5MC,则⊙O半径的长是3$\sqrt{5}$.
如图,⊙O的直径为CD,AB是⊙O的弦,AB⊥CD,垂足为M,AB=10,MD=5MC,则⊙O半径的长是3$\sqrt{5}$.
分析 连接OA,根据垂径定理得出AM的长,设CM=x,则DM=5x,OM=2x,根据勾股定理求出x的值即可.
解答  解:连接OA,
解:连接OA,
∵AB⊥CD,垂足为M,AB=10,
∴AM=BM=5.
∵MD=5MC,
∴设CM=x,则DM=5x,OM=2x,OA=3x,
∵AM2+OM2=OA2,即52+(2x)2=(3x)2,解得x=$\sqrt{5}$,
∴OA=3x=3$\sqrt{5}$.
故答案为:3$\sqrt{5}$.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
 图中一共有35条线段,一共有50个角(平角除外)
图中一共有35条线段,一共有50个角(平角除外)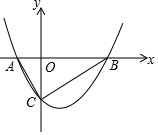 如图,抛物线y=$\frac{1}{2}$x2-x+a与x轴交于点A、B,与y轴交于点C,其顶点纵坐标为-2.
如图,抛物线y=$\frac{1}{2}$x2-x+a与x轴交于点A、B,与y轴交于点C,其顶点纵坐标为-2.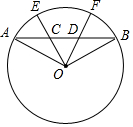 如图,AB为⊙O的弦,半径OE,OF分别交AB于点C,D,且OC=OD,求证:$\widehat{AE}$=$\widehat{BF}$.
如图,AB为⊙O的弦,半径OE,OF分别交AB于点C,D,且OC=OD,求证:$\widehat{AE}$=$\widehat{BF}$. 如图,在△ABC中,锐角∠C=θ°,BC=a,AC=b.
如图,在△ABC中,锐角∠C=θ°,BC=a,AC=b. 如图,已知点A(1,2),B(2,1),若点P是x轴上动点,点Q是y轴上动点,点P满足|PA-PB|的值最大,点Q满足QA+QB的值最小,则PQ=$\frac{\sqrt{106}}{3}$.
如图,已知点A(1,2),B(2,1),若点P是x轴上动点,点Q是y轴上动点,点P满足|PA-PB|的值最大,点Q满足QA+QB的值最小,则PQ=$\frac{\sqrt{106}}{3}$.