题目内容
19.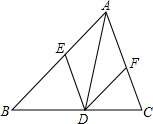 如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,当∠BAC=90°时,四边形AEDF是正方形.
如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,当∠BAC=90°时,四边形AEDF是正方形.
分析 当∠BAC=90°时,四边形AEDF是正方形,首先证明?AEDF为菱形,然后再根据有一个角为直角的菱形是正方形可得结论.
解答 解:当∠BAC=90°时,四边形AEDF是正方形;
理由:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
又∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴AE=DE.
∴?AEDF为菱形.
∵∠BAC=90°,
∴四边形AEDF是正方形,
故答案为:=90°.
点评 此题主要考查了正方形的判定,关键是掌握正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个矩形有一个角为直角.
③还可以先判定四边形是平行四边形,再用①或②进行判定.

练习册系列答案
相关题目
4.若关于x的方程$\frac{|x|}{x+4}$=kx2有四个不同的实数解,则k的取值范围为( )
| A. | (0,1) | B. | ($\frac{1}{4}$,1) | C. | ($\frac{1}{4}$,+∞) | D. | (1,+∞) |
11.已知一次函数y=ax+b(a,b是常数),x与y的部分对应值如下表:
那么代数式5a+b的值为-8.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
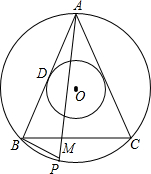 如图,已知△ABC内接于以点O为同心圆的大圆⊙O,且AB=AC,腰AB切小圆⊙O于点D.P是$\widehat{BC}$上的动点(不与点B、C重合),AP交BC于点M.
如图,已知△ABC内接于以点O为同心圆的大圆⊙O,且AB=AC,腰AB切小圆⊙O于点D.P是$\widehat{BC}$上的动点(不与点B、C重合),AP交BC于点M. 如图,P为菱形ABCD的对角线AC上一点,若PB=3,则PD=3.(填“>”或“=”或“<”号)
如图,P为菱形ABCD的对角线AC上一点,若PB=3,则PD=3.(填“>”或“=”或“<”号) 实数a,b在数轴上对应的位置如图示:
实数a,b在数轴上对应的位置如图示: