题目内容
10．先化简，再求值：$\frac{{x}^{2}}{x+1}-\frac{x}{x+1}$，其中x=-$\sqrt{5}$．分析 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．
解答 解：原式=$\frac{{x}^{2}-x}{x+1}$，
当x=-$\sqrt{5}$时，原式=$\frac{{（-\sqrt{5}）}^{2}+\sqrt{5}}{-\sqrt{5}+1}$=$\frac{5+\sqrt{5}}{-\sqrt{5}+1}$=$\frac{（5+\sqrt{5}）（1+\sqrt{5}）}{（1+\sqrt{5}）（1-\sqrt{5}）}$=-$\frac{5}{2}$-$\frac{3\sqrt{5}}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
初中暑期衔接系列答案
相关题目
18．
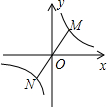如图，点M（2，a）在反比例函数y=$\frac{6}{x}$的图象上，连结MO并延长交图象的另一分支点N，则线段MN的长是（ ）
如图，点M（2，a）在反比例函数y=$\frac{6}{x}$的图象上，连结MO并延长交图象的另一分支点N，则线段MN的长是（ ）| A． | 3 | B． | $\sqrt{13}$ | C． | 6 | D． | 2$\sqrt{13}$ |
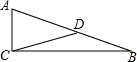如图，一位同学做了一个斜面装置进行科学实验，△ABC是该装置左视图，∠ACB=90°，∠B=15°，为了加固斜面，在斜面AB的中点D处连结一条支撑杆CD，量得CD=6．
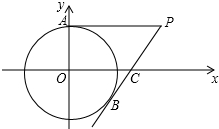如图，在平面直角坐标系中，以点O为圆心，半径为2的圆与y轴交于点A，点P（4，2）是⊙O外一点，连接AP，直线PB与⊙O相切于点B，交x轴于点C