题目内容
20.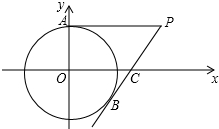 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C(1)证明PA是⊙O的切线;
(2)求直线AB的解析式.
分析 (1)由AO=2,P的纵坐标为2,得到AP与x轴平行,即PA与AO垂直,即可得到AP为圆O的切线;
(2)连接OP,OB,过B作BQ垂直于OC,由切线长定理得到PA=PB=4,PO为角平分线,进而得到一对角相等,根据AP与OC平行,利用两直线平行内错角相等得到一对角相等,等量代换并利用等角对等边得到OC=CP,设OC=x,BC=BP-PC=4-x,OB=2,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出OC与BC的长,在直角三角形OBC中,利用面积法求出BQ的长,再利用勾股定理求出OQ的长,根据B在第四象限,即可求出B的坐标,然后求得一次函数的解析式.
解答 (1)证明:∵圆O的半径为2,P(4,2),
∴AP⊥OA,
则AP为圆O的切线;
(2)解:连接OP,OB,过B作BQ⊥OC,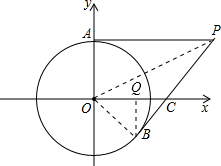 ∵PA、PB为圆O的切线,
∵PA、PB为圆O的切线,
∴∠APO=∠BPO,PA=PB=4,
∵AP∥OC,
∴∠APO=∠POC,
∴∠BPO=∠POC,
∴OC=CP,
在Rt△OBC中,设OC=PC=x,则BC=PB-PC=4-x,OB=2,
根据勾股定理得:OC2=OB2+BC2,即x2=4+(4-x)2,
解得:x=2.5,
∴BC=4-x=1.5,
∵S△OBC=$\frac{1}{2}$OB•BC=$\frac{1}{2}$OC•BQ,即OB•BC=OC•BQ,
∴BQ=$\frac{2×1.5}{2.5}$=1.2,
在Rt△OBQ中,根据勾股定理得:OQ=$\sqrt{O{B}^{2}-B{Q}^{2}}$=1.6,
则B坐标为(1.6,-1.2),
设直线AB的解析式为y=kx+b,
由A(0,2),B,(1.6,-1.2);可得$\left\{\begin{array}{l}{2=b}\\{-1.2=1.6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-2x+2.
点评 此题考查了切线的性质与判定,坐标与图形性质,勾股定理,三角形的面积求法,平行线的性质,以及切线长定理,待定系数法求一次函数的解析式,熟练掌握切线的性质与判定是解本题的关键.

 阅读快车系列答案
阅读快车系列答案| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 3 | 2 | 6 | 5 | 4 |
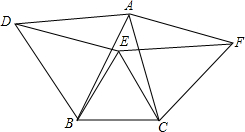 如图,以△ABC的三边分别作等边△ABD,△BCE,△ACF.
如图,以△ABC的三边分别作等边△ABD,△BCE,△ACF.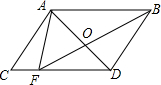 如图,平行四边形ABDC的面积为112平方厘米,又知AB=4CF,求三角形AOF的面积.
如图,平行四边形ABDC的面积为112平方厘米,又知AB=4CF,求三角形AOF的面积.
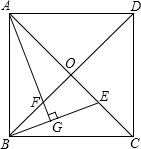 如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.