题目内容
5.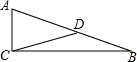 如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.
如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.(1)求斜坡AB长和∠ADC的度数;
(2)该同学想用彩纸实验装置中的△ABC的表面,请你计算△ABC的面积.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半可得AB=2CD,然后根据等腰三角形的性质即可得到结论;
(2)过C作CE⊥AB于E,根据直角三角形的性质得到CE=$\frac{1}{2}$CD=3,由三角形的面积公式即可得到结论.
解答 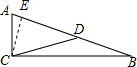 解:(1)∵∠ACB=90°,D是AB的中点,
解:(1)∵∠ACB=90°,D是AB的中点,
∴AB=2CD=2×6=12,
∵CD=BD,
∴∠ADC=2∠B=30°;
(2)过C作CE⊥AB于E,
∵∠ADC=30°,
∴CE=$\frac{1}{2}$CD=3,
∴S△ABC=$\frac{1}{2}$×12×3=18.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,含30°角的直角三角形的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | a3+a3=a6 | B. | 4ab÷2a=2ab | C. | a3•a4=a7 | D. | (3x2)3=9x6 |
17. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠1与∠C是同位角 | B. | ∠1与∠3是对顶角 | ||
| C. | ∠3与∠C是内错角 | D. | ∠B与∠3是同旁内角 |
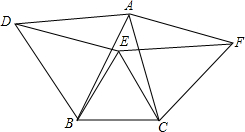 如图,以△ABC的三边分别作等边△ABD,△BCE,△ACF.
如图,以△ABC的三边分别作等边△ABD,△BCE,△ACF.