题目内容
已知二次函数y=x2-4x+3.
(1)求二次函数与x轴的交点坐标;
(2)求二次函数的对称轴和顶点坐标;
(3)写出y随x增大而减小时自变量x的取值范围.
(1)求二次函数与x轴的交点坐标;
(2)求二次函数的对称轴和顶点坐标;
(3)写出y随x增大而减小时自变量x的取值范围.
考点:抛物线与x轴的交点,二次函数的性质
专题:计算题
分析:(1)根据抛物线与x轴的交点问题,解方程x2-4x+3=0即可得到二次函数与x轴的交点坐标;
(2)先把解析式配成顶点式,然后根据二次函数的性质得到二次函数的对称轴和顶点坐标;
(3)根据二次函数的性质求解.
(2)先把解析式配成顶点式,然后根据二次函数的性质得到二次函数的对称轴和顶点坐标;
(3)根据二次函数的性质求解.
解答:解:(1)当y=0时,x2-4x+3=0,解得x1=1,x2=3,
所以二次函数与x轴的交点坐标为(1,0),(3,0);
(2)y=x2-4x+3=(x-2)2-1,
所以二次函数的对称轴为直线x=2,顶点坐标为(2,-1);
(3)当x<2时,y随x增大而减小.
所以二次函数与x轴的交点坐标为(1,0),(3,0);
(2)y=x2-4x+3=(x-2)2-1,
所以二次函数的对称轴为直线x=2,顶点坐标为(2,-1);
(3)当x<2时,y随x增大而减小.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.

练习册系列答案
相关题目
方程x2-9x+18=0的两个根是等腰三角形的底和腰,则这个三角形是周长是( )
| A、12 | B、15 |
| C、12或15 | D、9或15或18 |
下列有关向量的等式中,不一定成立的是( )
A、
| ||||||||
B、|
| ||||||||
C、
| ||||||||
D、|
|
抛物线y=-x2不具有的性质是( )
| A、开口向上 |
| B、对称轴是y轴 |
| C、在对称轴的左侧,y随x的增大而增大 |
| D、最高点是原点 |
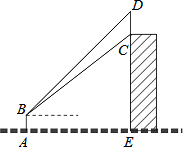 如图,某幢大楼的外墙边上竖直安装着一根旗杆CD,小明在离旗杆下方大楼底部E点24米的点A处放置一台测角仪,测角仪的高度AB为1.5米,并在点B处测得旗杆下端C的仰角为40°,上端D的仰角为45°,求旗杆CD的长度;(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
如图,某幢大楼的外墙边上竖直安装着一根旗杆CD,小明在离旗杆下方大楼底部E点24米的点A处放置一台测角仪,测角仪的高度AB为1.5米,并在点B处测得旗杆下端C的仰角为40°,上端D的仰角为45°,求旗杆CD的长度;(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)