题目内容
方程x2-9x+18=0的两个根是等腰三角形的底和腰,则这个三角形是周长是( )
| A、12 | B、15 |
| C、12或15 | D、9或15或18 |
考点:解一元二次方程-因式分解法,三角形三边关系,等腰三角形的性质
专题:
分析:先求出方程的解,得出三角形的三边长,看看是否符合三角形的三边关系定理,求出即可.
解答:解:x2-9x+18=0,
(x-3)(x-6)=0,
x-3=0,x-6=0,
x1=3,x2=6,
有两种情况:①三角形的三边为3,3,6,此时不符合三角形三边关系定理,
②三角形的三边为3,6,6,此时符合三角形三边关系定理,此时三角形的周长为3+6+6=15,
故选B.
(x-3)(x-6)=0,
x-3=0,x-6=0,
x1=3,x2=6,
有两种情况:①三角形的三边为3,3,6,此时不符合三角形三边关系定理,
②三角形的三边为3,6,6,此时符合三角形三边关系定理,此时三角形的周长为3+6+6=15,
故选B.
点评:本题考查了三角形的三边关系定理,等腰三角形的性质,解一元二次方程的应用,解此题的关键是求出三角形的三边长,难度适中.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
下列运算中,不正确的是( )
| A、(-a3)2=a9 |
| B、a3+a3=2a3 |
| C、a2•a3=a5 |
| D、2a3÷a2=2a |
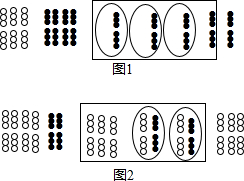 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )
我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )| A、(-5)+(-2) |
| B、(-5)+2 |
| C、5+(-2) |
| D、5+2 |
已知二次函数y=ax2-2x+2(a>0),那么它的图象一定不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在平面直角坐标系xOy中,点A(
如图,在平面直角坐标系xOy中,点A(