题目内容
8.计算:(1)(x-$\frac{1}{y}$)÷(y-$\frac{1}{x}$);
(2)($\frac{3a}{a+2}$-$\frac{a}{a-2}$)÷$\frac{2a}{{a}^{2}-4}$.
分析 (1)先算括号内的减法,再把除法变成乘法,最后求出即可;
(2)先算括号内的减法,再把除法变成乘法,最后求出即可.
解答 解:(1)原式=$\frac{xy-1}{y}$÷$\frac{xy-1}{x}$
=$\frac{xy-1}{y}$•$\frac{x}{xy-1}$
=$\frac{x}{y}$;
(2)原式=$\frac{3a(a-2)-a(a+2)}{(a+2)(a-2)}$•$\frac{(a+2)(a-2)}{2a}$
=$\frac{2a(a-4)}{(a+2)(a-2)}$•$\frac{(a+2)(a-2)}{2a}$
=a-4.
点评 本题考查了分式的混合运算的应用,能熟练地运用法则进行计算是解此题的关键.

练习册系列答案
相关题目
18.由二次函数y=3(x-2)2+1可知( )
| A. | 图象的开口向下 | B. | 图象的对称轴是直线x=-2 | ||
| C. | 函数最小值为1 | D. | 当x<2时,y随x的增大而增大 |
16.我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示是( )
| A. | 0.675×105 | B. | 67.5×103 | C. | 6.75×104 | D. | 6.75×105 |
3.景德镇昌河汽车制造厂本周计划每日生产100辆北斗星小轿车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如表(增加的辆数为正数,减少的辆数为负数)
根据记录回答:
(1)本周生产了多少辆小轿车?
(2)本周总生产量与计划量相比是增加了还是减少了?增加或减少了多少辆?
(3)生产量最多的一天比生产量最少的一天多生产多少辆?
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增 减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周生产了多少辆小轿车?
(2)本周总生产量与计划量相比是增加了还是减少了?增加或减少了多少辆?
(3)生产量最多的一天比生产量最少的一天多生产多少辆?
20.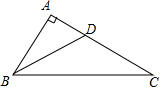 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )
 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D,且AD=5cm,AB=12cm,BD=13cm,则点D到BC的距离是( )| A. | 5cm | B. | 12cm | C. | 13cm | D. | 不能确定 |
17.下列方程是一元一次方程的是( )
| A. | $\frac{2}{y}$=1 | B. | 3x+2y=0 | C. | x2-l=0 | D. | x=3 |
18.为了创建“全国文明城市”,我校志愿者小组成员从学校出发,在学校门口东西方向的道路上进行义务保洁.规定向东行为正,向西行为负,已知某志愿者一个下午的七次行走记录如表所示(单位:千米):
(1)该志愿者保洁结束时是否回到出发地点?如果没有,那么距离出发点多少千米?
(2)在第六次保洁时离出发地点最远;
(3)若每千米平均用时15分钟,则该志愿者完成这次保洁任务一共用时多少小时?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| +1 | -1.1 | +2 | +0.7 | -1 | +1.2 | -3 |
(2)在第六次保洁时离出发地点最远;
(3)若每千米平均用时15分钟,则该志愿者完成这次保洁任务一共用时多少小时?
 如图的数阵由若干个偶数排成.
如图的数阵由若干个偶数排成.