题目内容
13.直角三角形的两边长分别为5和12,则此三角形的外接圆半径是$\frac{13}{2}$或6.分析 分为两种情况,①当斜边是12时,②当两直角边是5和12时,求出即可.
解答 解:分为两种情况:①当斜边是12cm时,直角三角形的外接圆的半径是$\frac{1}{2}$×12=6;
②当两直角边是5cm和12cm时,由勾股定理得:斜边为$\sqrt{{5}^{2}+1{2}^{2}}$=13,
直角三角形的外接圆的半径是$\frac{1}{2}$×13=$\frac{13}{2}$;
故答案为$\frac{13}{2}$或6.
点评 本题考查了直角三角形的性质,勾股定理,三角形的外接圆的应用,注意:直角三角形的外接圆的半径等于斜边的一半.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
3.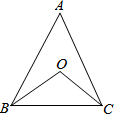 如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
 如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 2α° | B. | (α+60)° | C. | (α+90)° | D. | ($\frac{1}{2}$α+90)° |
4.抛物线y=-3x2+2x-l的图象与坐标轴的交点个数是( )
| A. | 无交点 | B. | 1个 | C. | 2个 | D. | 3个 |
5.下列计算中,正确的是( )
| A. | 7ab-3ab=4 | B. | -$\frac{1}{3}$(6a-1)=-2a+1 | C. | x2y-2x2y=-x2y | D. | (-$\frac{1}{2}$)÷$\frac{1}{4}$×2=-1 |
2.在下列说法中,正确的是( )
| A. | 如果两个三角形全等,则它们一定能关于某直线成轴对称 | |
| B. | 如果两个三角形关于某直线成轴对称,那么它们是全等三角形 | |
| C. | 等腰三角形的对称轴是底边上的高 | |
| D. | 若两个图形关于某直线对称,则它们的对应点一定位于对称轴的两侧 |
3.计算6a3÷(-2a)的结果是( )
| A. | -3a2 | B. | -3a3 | C. | 3a2 | D. | 3a |
