题目内容
14.某住宅小区将现有一块三角形的绿化地改造为一块圆形的绿化地(如图1,已知原来三角形绿化地中道路AB长为16$\sqrt{2}$米,在点B的拐弯处道路AB与BC所夹的∠B为45°,在点C的拐弯处道路AC与BC所夹的∠C的正切值为2(即tan∠C=2),如图2;(1)求拐弯点B与C之间的距离;
(2)在改造好的圆形(圆O)绿化地中,这个圆O过点A、C,并与原道路BC交于点D,如果点A是圆弧(优弧)道路DC的中点,求圆O的半径长.
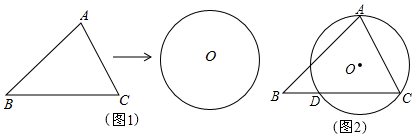
分析 (1)如图1中,作AE⊥BC于E.分别求出BE、EC即可解决问题;
(2)如图2中,连接AO,延长AO交BC于E,连接OC.首先证明AE⊥BC,在Rt△OEC中,利用勾股定理构建方程即可解决问题;
解答 解:(1)如图1中,作AE⊥BC于E.
在Rt△ABE中,∵∠AEB=90°,∠B=45°,AB=16$\sqrt{2}$,
∴AE=BE=16,
在Rt△AEC中,tanc=$\frac{AE}{EC}$=2,
∴$\frac{16}{EC}$=2,
∴EC=8,
∴BC=BE+CE=16+8=24.
(2)如图2中,连接AO,延长AO交BC于E,连接OC.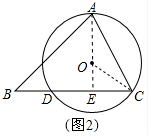
∵$\widehat{AD}$=$\widehat{AC}$,
∴AE⊥CD,设OA=OC=R,
在Rt△OEC中,∵OE2+EC2=OC2,
∴(16-R)2+82=R2,
∴R=10,
∴⊙O的半径为10.
点评 本题考查圆的有关知识、解直角三角形、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目



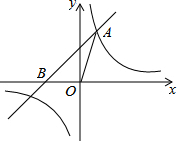 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交x轴于点B.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交x轴于点B. 如图,∠1=75°,∠2=105°,AB与ED平行吗?为什么?
如图,∠1=75°,∠2=105°,AB与ED平行吗?为什么? 计算图中阴影部分的面积.
计算图中阴影部分的面积.