题目内容
15.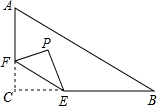 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )| A. | 3.2 | B. | 2 | C. | 1.2 | D. | 1 |
分析 如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小,利用△AFM∽△ABC,得到$\frac{AF}{AB}=\frac{FM}{BC}$求出FM即可解决问题.
解答 解:如图,延长FP交AB于M,当FP⊥AB时,点P到AB的距离最小.(点P在以F为圆心CF为半径的圆上,当FP⊥AB时,点P到AB的距离最小)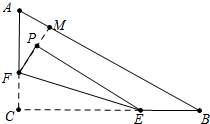
∵∠A=∠A,∠AMF=∠C=90°,
∴△AFM∽△ABC,
∴$\frac{AF}{AB}=\frac{FM}{BC}$,
∵CF=2,AC=6,BC=8,
∴AF=4,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∴$\frac{4}{10}$=$\frac{FM}{8}$,
∴FM=3.2,
∵PF=CF=2,
∴PM=1.2
∴点P到边AB距离的最小值是1.2.
故选C.
点评 本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理.垂线段最短等知识,解题的关键是正确找到点P位置,属于中考常考题型.

练习册系列答案
相关题目
3.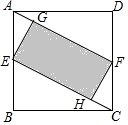 如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
 如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )| A. | y=3$\sqrt{3}$x2 | B. | y=4$\sqrt{3}$x2 | C. | y=8x2 | D. | y=9x2 |
 在?ABCD中,∠BAD的平分线AE交BC于点E,BE=3,若?ABCD的周长是16,则EC=2.
在?ABCD中,∠BAD的平分线AE交BC于点E,BE=3,若?ABCD的周长是16,则EC=2.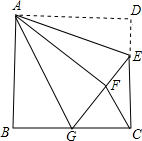 如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.
如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.
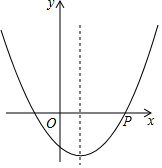 如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(5,0)在抛物线上,则9a-3b+c的值0.
如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(5,0)在抛物线上,则9a-3b+c的值0.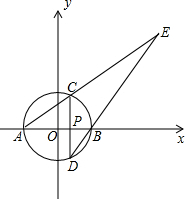 如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.