一些完全相同的小正方体搭成一个几何体.这个几何体从正面和左面看所得的平面图形均为如图.小正方体的块数最多有( ) A.11块B.12块C.13块D.14块题目和参考答案——青夏教育精英家教网—

题目内容

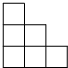一些完全相同的小正方体搭成一个几何体，这个几何体从正面和左面看所得的平面图形均为如图，小正方体的块数最多有（　　）

A、11块	B、12块
C、13块	D、14块

考点：由三视图判断几何体

专题：

分析：从正面看得到的图形表现了几何体的长与高，从左面看得到的图形表现了几何体的宽和高，得到组合几何体的正方体的最多的个数即可．

解答：解：由2个视图可得该组合几何体有3行，3列，
所以最底层最多有9个正方体；
第二层最多有4个正方体；
第3层最多有1个正方体，所以组合几何体最多有9+4+1=14个正方体．
故选D．

点评：考查了由三视图判断几何体；得到组合几何体的正方体的最多的个数和最少的个数是解决本题的关键．

练习册系列答案

相关题目

一个两位数，十位数字是x，个位数字是y，如果在它们中间加上一个0得到的数是（　　）

在实数范围内有意义，则x的取值范围是（　　）

A、x＜2	B、x≠-2
C、x＞2	D、x≤2

如图①，在梯形ABCD中，AD∥BC，∠A=60°，动点P从A点出发，以1cm/s的速度沿着A→B→C→D的方向不停移动，直到点P到达点D后才停止．已知△PAD的面积S （单位：cm²）与点P移动的时间t（单位：s）的函数关系如图②，则：
（1）BC=2cm；（2）梯形的面积是3

cm²；（3）∠ADC=30°；（4）点P从开始移动到停止移动一共用了7秒．
说法中正确的个数是（　　）

如图，在平面直角坐标中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，∠COA=60°，点P为x轴上的一个动点，点P不与点O、点A重合．连结CP，过点P作PD交AB于点D．若△OCP为等腰三角形，点P的坐标为（　　）

已知x=1是二次方程（m²-1）x²-mx+m²=0的一个根，那么m的值是（　　）

如图，△AOB是由△A₁O₁B₁平移后得到的，已知点A₁的坐标为（-3，-1）．
（1）求O₁，B₁的坐标；
（2）指出△A₁O₁B₁经过怎样的平移得到△AOB？

试题分类