题目内容
如图①,将一张直角△ABC纸片折叠,使点A与点C重合,这时DE为折痕,△ECB为等腰三角形;继续将纸片沿△ECB的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的矩形为“叠加矩形”.
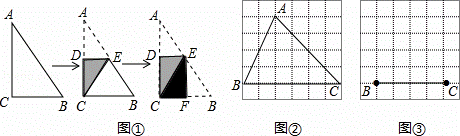
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕.
(2)如图③在正方形网格中,以给定的BC为一边,画出一个斜三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
(3)若一个三角形所折成的“叠加矩形”为正方形,那么必须满足的条件是什么?
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是什么?
考点: 几何变换综合题.
分析: (1)图2中将三角形的三个角分别向三角形内部进行折叠即可;
(2)图3中只要使三角形一边上的高等于该边长即可;
(3)利用折叠后的两个重合的正方形可知,三角形一边长的一半和这一边上的高的一半都等于正方形的边长,所以三角形的一边和这边上的高应该相等;
(4)如果一个四边形能折叠成叠加矩形,可以将四边形的四个角分别向四边形内部折叠即可得到该结果,折痕应经过四边中点,而连接四边形各边中点得到矩形的话,该四边形的对角线应互相垂直.
解答: 解:(1)(2)

(3)一边长与该边上的高相等的直角三角形或锐角三角形;
(4)对角线互相垂直.
点评: 此题考查是几何变换问题,是一道操作题,一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.关键是在操作的过程中,应善于分析图形,结合中点即可解决问题.

练习册系列答案
相关题目
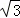 )是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=
)是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=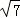 ;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).
;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).
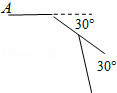
 =
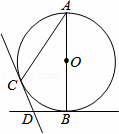
= .证明∠DGA+∠BAC=180°.
.证明∠DGA+∠BAC=180°. 