题目内容
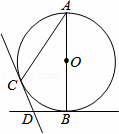
如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 °.
35
考点: 切线的性质;圆周角定理.
专题: 几何图形问题.
分析: 首先连接OC,由BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°,可求得∠BOC的度数,又由圆周角定理,即可求得答案.
解答: 解:连接OC,
∵BD,CD分别是过⊙O上点B,C的切线,
∴OC⊥CD,OB⊥BD,
∴∠OCD=∠OBD=90°,
∵∠BDC=110°,
∴∠BOC=360°﹣∠OCD﹣∠BDC﹣∠OBD=70°,
∴∠A= ∠BOC=35°.
∠BOC=35°.
故答案为:35.

点评: 此题考查了切线的性质以及圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
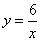 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线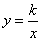 上运动,则
上运动,则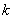 的值是 .
的值是 .


 +2﹣x)÷
+2﹣x)÷ ,其中x满足x2﹣4x+3=0.
,其中x满足x2﹣4x+3=0.
