题目内容
12.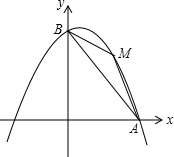 如图,抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点.
如图,抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点.(1)求a、b的值,并写出抛物线的解析式;
(2)记抛物线的顶点为C,求△ABC的面积;
(3)M是抛物线上的一个动点,且位于笫一象限内.设△ABM的面积为S,试求S的最大值.
分析 (1)把A和B点的坐标代入抛物线y=a(x-1)2+b,求出a,b的值,从而求出抛物线的解析式;
(2)过点C作CD⊥x轴于点D,根据抛物线的顶点坐标求出C的坐标,再根据S△ABC=S梯形BODC+S△ADC-S△AOB,即可求出△ABC的面积;
(3)过点M作MN⊥OA于N,设点M的坐标为[a,-$\frac{1}{2}$(a-1)2+$\frac{9}{2}$],根据M位于笫一象限,得出S△ABM=S梯形BONM+S△ANM-S△AOB,再把相关的数据代入计算即可得出答案.
解答 解:(1)∵抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点,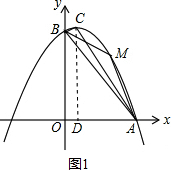
∴$\left\{\begin{array}{l}{0=a(4-1)^{2}+b}\\{4=a(0-1)^{2}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{9}{2}}\end{array}\right.$,
∴抛物线的解析式是y=-$\frac{1}{2}$(x-1)2+$\frac{9}{2}$;
(2)如图1,过点C作CD⊥x轴于点D,
∵抛物线的顶点是(1,$\frac{9}{2}$)
∴C的坐标是(1,$\frac{9}{2}$)
∴S△ABC=S梯形BODC+S△ADC-S△AOB
=$\frac{1}{2}$(CD+BO)•OD+$\frac{1}{2}$AD•CD-$\frac{1}{2}$AO•BO
=$\frac{1}{2}$($\frac{9}{2}$+4)×1+$\frac{1}{2}$×3×$\frac{9}{2}$-$\frac{1}{2}$×4×4
=3;
(3)如图2,过点M作MN⊥OA于N,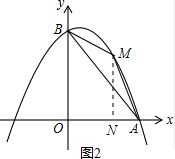
设点M的坐标为[a,-$\frac{1}{2}$(a-1)2+$\frac{9}{2}$],
∵M位于笫一象限,
∴S△ABM=S梯形BONM+S△ANM-S△AOB
=$\frac{1}{2}$×[4-$\frac{1}{2}$(a-1)2+$\frac{9}{2}$]•a+$\frac{1}{2}$×(4-a)×[-$\frac{1}{2}$(a-1)2+$\frac{9}{2}$]-$\frac{1}{2}$×4×4
=-a2+4a
=-(a-2)2+4,
∴S的最大值是4.
点评 此题考查了二次函数的综合,用到的知识点是三角形、梯形的面积公式、二次函数的图象与性质,关键是根据题意作出辅助线,构造梯形和直角三角形.

 教学练新同步练习系列答案
教学练新同步练习系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | $\sqrt{0.1}$ | B. | $\sqrt{19}$ | C. | $\sqrt{8}$ | D. | $\sqrt{4\frac{1}{4}}$ |