题目内容
3．不透明的口袋里装有除颜色外其余都相同的红球2个、黄球3个，若从中依次不放回的任意摸出二个球，则摸到不同颜色球的概率是$\frac{3}{5}$．分析 先画树状图展示所有20种等可能的结果数，再找出两个球的颜色不同的结果数，然后根据概率公式计算．
解答 解：画树状图为：
共有20种等可能的结果数，其中两个球的颜色不同的结果数为12，
所以摸到不同颜色球的概率=$\frac{12}{20}$=$\frac{3}{5}$．
故答案为$\frac{3}{5}$．
点评 本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
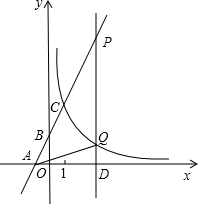如图，在平面直角坐标系xOy中，直线y=2x+n与x轴、y轴分别交于点A、B，与双曲线y=$\frac{4}{x}$在第一象限内交于点C（1，m）．
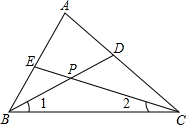如图，△ABC的角平分线BD、CE相交于点P，∠A=70°，求∠BPC的度数．
12．在具备下列条件的△ABC中，不是直角三角形的是（ ）
| A． | ∠A+∠B=∠C | B． | ∠A=3∠C，∠B=2∠C | C． | ∠A=∠B=2∠C | D． | ∠A=∠B=$\frac{1}{2}$∠C |