题目内容
11.判断下列二次函数的图象与x轴有无交点?若有,求出交点坐标;若没有,说明理由.(1)y=x2-2x-3.
(2)y=x2-x+3.
(3)y=4x2-4x+1.
(4)y=-$\frac{1}{2}$x2+x-4.
分析 首选判断△=b2-4ac的符号,若△<0则二次函数与x中没有交点,若△≥0,则有交点,然后令y=0求得抛物线与x轴的交点的横坐标即可.
解答 解:(1)△=4+12=16>0,则抛物线与z轴有两个交点,
令y=0,则x2-2x-3=0,解得x1=-1,x2=3,则交点坐标是(-1,0)和(3,0);
(2)△=1-12=-11<0,则抛物线与x轴没有交点;
(3)△=16-16=0,抛物线与x中只有一公共点.
令y=0,则4x2-4x+1=0,
解得:x1=x2=$\frac{1}{2}$.则交点坐标是($\frac{1}{2}$,0);
(4)△=1-4×(-$\frac{1}{2}$)×(-4)=1-8=-7<0,则二次函数与x轴没有交点.
点评 本题考查了二次函数与x轴的交点坐标的判断,可以利用判别式△判断,另外求函数与x轴的交点坐标的方法也是经常考的内容.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.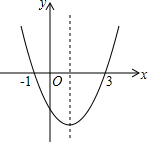 如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
 如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.有理数-1,-(-12),-|-12|,按从小到大的顺序排列为( )
| A. | -1<-(-12)<-|-12| | B. | -(-12)<-|-12|<-1 | C. | -|-12|<-1<-(-12) | D. | -|-12|<-(-12)<-1 |
 如图,M是线段AB的中点,点C在线段AB上,N是AC的中点,且AN=2cm,CM=1cm,求线段AB的长.
如图,M是线段AB的中点,点C在线段AB上,N是AC的中点,且AN=2cm,CM=1cm,求线段AB的长. 二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.
二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.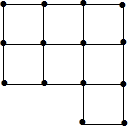 如图所示是由20根小棒摆成的大小相同的7个正方形,很明显它不是轴对称图形,请你将一根小棒移动到合适的位置,使移动后的图形成为一个轴对称图形.
如图所示是由20根小棒摆成的大小相同的7个正方形,很明显它不是轴对称图形,请你将一根小棒移动到合适的位置,使移动后的图形成为一个轴对称图形.