题目内容
15.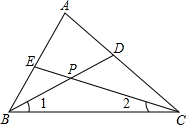 如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数.
如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数.
分析 先利用角平分线的定义得到∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,则利用三角形内角和定理得到∠BPC=180°-$\frac{1}{2}$(∠ABC+∠ACB),二∠ABC+∠ACB=180°-∠A=110°,所以∠BPC=180°-$\frac{1}{2}$×110°=125°.
解答 解:∵△ABC的角平分线BD、CE相交于点P,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,
∵∠BPC+∠1+∠2=180°,
∴∠BPC=180°-$\frac{1}{2}$(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∴∠BPC=180°-$\frac{1}{2}$×110°=125°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.本题的关键是利用三角形内角和把∠BPC与∠A联系起来.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.
二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.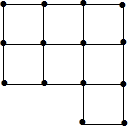 如图所示是由20根小棒摆成的大小相同的7个正方形,很明显它不是轴对称图形,请你将一根小棒移动到合适的位置,使移动后的图形成为一个轴对称图形.
如图所示是由20根小棒摆成的大小相同的7个正方形,很明显它不是轴对称图形,请你将一根小棒移动到合适的位置,使移动后的图形成为一个轴对称图形. 如图,OA⊥AC,OB⊥BC,若∠1=∠2,则AC=BC.
如图,OA⊥AC,OB⊥BC,若∠1=∠2,则AC=BC.