题目内容
14.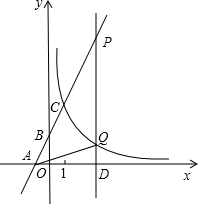 如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=$\frac{4}{x}$在第一象限内交于点C(1,m).
如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=$\frac{4}{x}$在第一象限内交于点C(1,m).(1)求m和n的值;
(2)过x轴上的点D(a,0)作平行于x轴的直线l(a>1),分别与直线AB和双曲线y=$\frac{4}{x}$交于点P、Q,且PQ=2QD,求△APQ的面积.
分析 (1)由直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=$\frac{4}{x}$在第一象限内交于点C(1,m).把C(1,m)代入y=$\frac{4}{x}$,得m=4,把C(1,4)代入y=2x+n中得n=2;
(2)在y=2x+2中,令y=0,则x=-1,求得A(-1,0),求出P(a,2a+2),Q(a,$\frac{4}{a}$),根据PQ=2QD,列方程2a+2-$\frac{4}{a}$=2×$\frac{4}{a}$,解得a=2,a=-3,即可得到结果.
解答 解:(1)∵直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=$\frac{4}{x}$在第一象限内交于点C(1,m).
∴把C(1,m)代入y=$\frac{4}{x}$,得m=4,
∴C(1,4),
把C(1,4)代入y=2x+n中得n=2,
∴m和n的值分别为:4,2;
(2)在y=2x+2中,令y=0,则x=-1,
∴A(-1,0),
∵D(a,0),l∥y轴,
∴P(a,2a+2),Q(a,$\frac{4}{a}$),
∵PQ=2QD,
∴2a+2-$\frac{4}{a}$=2×$\frac{4}{a}$,
解得:a=2,a=-3,
∵点P,Q在第一象限,
∴a=2,
∴PQ=4,
又∵AD=3
∴S△APQ=$\frac{1}{2}$×4×3=6.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求函数解析式.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
2.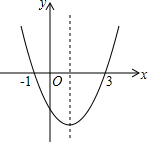 如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
 如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
如图,为二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②方程ax2+bx+c=0的根为x1=-1,x2=-3;③a+b+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.计算$\root{3}{27}$的结果是( )
| A. | ±3 | B. | 3 | C. | 3$\sqrt{3}$ | D. | $\sqrt{3}$ |
 二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积.
二次函数y=x2+4x+3的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求:四边形ACBD的面积. 如图,OA⊥AC,OB⊥BC,若∠1=∠2,则AC=BC.
如图,OA⊥AC,OB⊥BC,若∠1=∠2,则AC=BC.