��Ŀ����
14�� ���壺�������������ڽǵĶ����ֱ���x��y��z������x2+y2=z2��������������Ϊ���������Σ�
���壺�������������ڽǵĶ����ֱ���x��y��z������x2+y2=z2��������������Ϊ���������Σ���1�������������壬��ֱ���������ǹ��������Ρ���������Ǽ����⣻
��2����֪һ���������������ڽǴ�С��������Ϊx��y��z����xy=2160����x+y��ֵ��
��3����ͼ����ABC�У�AB=$\sqrt{6}$��BC=2��AC=1+$\sqrt{3}$����֤����ABC�ǹ��������Σ�
���� ��1��ֱ�Ӹ��ݡ����������Ρ��Ķ��壬�жϵó����ɣ�
��2��������֪�ó���������ϵ��ɷ����飬�������x+y��ֵ��
��3����B��BH��AC��H����AH=x�����ù��ɶ������ȵó�AH=BH=$\sqrt{3}$��HC=1�������ó���A=45�㣬��C=60�㣬��B=75�㣬���ɵó����ۣ�
��� ��1���⣺��ֱ���������ǹ��������Ρ��Ǽ����⣻�������£�
�߶�������������Σ����������ǵĶ����ֱ�Ϊx�㡢y���z�㣬
������x2+y2=z2������������������������
�����õ�������ֱ���������ǹ��������Σ����Ǽ����⣻
��2���⣺������ɵã�$\left\{\begin{array}{l}{x+y+z=180}&{\;}\\{xy=2160}&{\;}\\{{x}^{2}+{y}^{2}={z}^{2}}&{\;}\end{array}\right.$��
��ã�x+y=102��
��3��֤������B��BH��AC��H����ͼ��ʾ��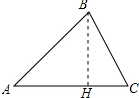
��AH=x
Rt��ABH��BH=$\sqrt{6-{x}^{2}}$��
Rt��CBH����$\sqrt{6-{x}^{2}}$��2+��1+$\sqrt{3}$-x��2=4��
��ã�x=$\sqrt{3}$��
��AH=BH=$\sqrt{3}$��HC=1��
���A=��ABH=45�㣬
��tan��HBC=$\frac{HC}{BH}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$��
���HBC=30�㣬
���BCH=60�㣬��B=75�㣬
��452+602=752
���ABC�ǹ��������Σ�
���� ������Ҫ�������¶��塢��Ԫ������ⷨ�����ɶ�����������Ǻ�����ϵ�����ù��ɶ����ó�AH��HC�ij��ǽ���ؼ���

 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�| A�� | -1 | B�� | 1 | C�� | -2 | D�� | 2 |
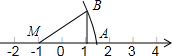 ��ͼ��Rt��MBC�У���MCB=90�㣬��M������-1������C������1����MA=MB��BC=1���������ϵ�A��Ӧ�����ǣ�������
��ͼ��Rt��MBC�У���MCB=90�㣬��M������-1������C������1����MA=MB��BC=1���������ϵ�A��Ӧ�����ǣ�������| A�� | $\sqrt{5}$+1 | B�� | -$\sqrt{5}$+1 | C�� | -$\sqrt{5}$-l | D�� | $\sqrt{5}$-1 |
 ��ͼ��AB��CD��EF��MN��Ϊֱ�ߣ���2=��3=70�㣬��GPC=80�㣬GHƽ�֡�MGB�����1=��������
��ͼ��AB��CD��EF��MN��Ϊֱ�ߣ���2=��3=70�㣬��GPC=80�㣬GHƽ�֡�MGB�����1=��������| A�� | 35�� | B�� | 40�� | C�� | 45�� | D�� | 50�� |
 ��ͼ��AB�ǡ�O��ֱ����AC���ң��뾶OD��AC�ڵ�E������D��������BA�ӳ��߽��ڵ�F��
��ͼ��AB�ǡ�O��ֱ����AC���ң��뾶OD��AC�ڵ�E������D��������BA�ӳ��߽��ڵ�F�� ��ͼ����֪��ABC�ס�ACP��AB=5��AC=2�����ABC���ACP���ܳ�֮��Ϊ5��2��
��ͼ����֪��ABC�ס�ACP��AB=5��AC=2�����ABC���ACP���ܳ�֮��Ϊ5��2��