题目内容
19.△ABC,∠A、∠B、∠C的对边分别是a、b、c,一条直线DE与边AC相交于点D,与边AB相交于点E.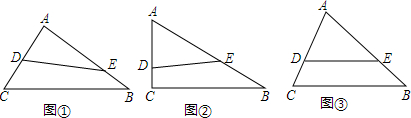
(1)如图①,若DE将△ABC分成周长相等的两部分,则AD+AE等于多少;(用a、b、c表示)
(2)如图②,若AC=3,AB=5,BC=4.DE将△ABC分成周长、面积相等的两部分,求AD;
(3)如图③,若DE将△ABC分成周长、面积相等的两部分,且DE∥BC,则a、b、c满足什么关系?
分析 (1)由DE将△ABC分成周长相等的两部分,于是得到AD+AE=CD+BC+BE=$\frac{1}{2}$(AB+AC+BC)=$\frac{1}{2}$(a+b+c);
(2)设AD=x,AE=6-x,根据三角形的面积公式列方程得到$\frac{1}{2}$x(6-x)•$\frac{4}{5}$=3,解得x1=$\frac{6+\sqrt{6}}{2}$(舍去),x2=$\frac{6-\sqrt{6}}{2}$,即可得到结论;
(3)由DE∥BC,推出△ADE∽△ABC,根据相似三角形的性质得到$\frac{AD}{AC}=\frac{AE}{AB}$,由$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{2}$即可得到结论.
解答 解:(1)∵DE将△ABC分成周长相等的两部分,
∴AD+AE=CD+BC+BE=$\frac{1}{2}$(AB+AC+BC)=$\frac{1}{2}$(a+b+c);
(2)设AD=x,AE=6-x,
∵S△ADE=$\frac{1}{2}$AD•AE•sinA=3,
即:$\frac{1}{2}$x(6-x)•$\frac{4}{5}$=3,
解得:x1=$\frac{6+\sqrt{6}}{2}$(舍去),x2=$\frac{6-\sqrt{6}}{2}$,
∴AD=$\frac{6-\sqrt{6}}{2}$;
(3)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AC}=\frac{AE}{AB}$,
∵$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{2}$,
∴AD=$\frac{\sqrt{2}}{2}$b,AE=$\frac{\sqrt{2}}{2}$c,
∴$\frac{\sqrt{2}}{2}$b$+\frac{\sqrt{2}}{2}$c=$\frac{1}{2}$(a+b+c),
∴$\frac{a}{b+c}$=$\sqrt{2}$-1.
点评 本题考查了相似三角形的判定和性质,三角形的周长和面积的计算,熟练掌握相似三角形的判定和性质是解题的关键.

| A. | A、B两点间的距离 | B. | A、C两点间的距离 | ||
| C. | A、B两点到原点的距离之和 | D. | A、C两点倒原点的距离之和 |
 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是( )| A. | DF⊥AB | B. | CG=2GA | C. | CG=DF+GE | D. | S四边形BFGC=$\sqrt{3}$-1 |
 如图,l∥m,等边△ABC的顶点A在直线m上,CB的延长线交m于点D,则∠α=20°.
如图,l∥m,等边△ABC的顶点A在直线m上,CB的延长线交m于点D,则∠α=20°. 定义:若三角形三个内角的度数分别是x、y和z,满足x2+y2=z2,则称这个三角形为勾股三角形.
定义:若三角形三个内角的度数分别是x、y和z,满足x2+y2=z2,则称这个三角形为勾股三角形. 在如图所示的数轴上,点C与点B关于点A对称,C、A两点对应的实数分别是$\sqrt{5}$和1,则点B对应的实数为2-$\sqrt{5}$.
在如图所示的数轴上,点C与点B关于点A对称,C、A两点对应的实数分别是$\sqrt{5}$和1,则点B对应的实数为2-$\sqrt{5}$. 如图,∠AOC和∠DOB都是直角,如果∠DOC=35°,那么∠AOB的度数为145°.
如图,∠AOC和∠DOB都是直角,如果∠DOC=35°,那么∠AOB的度数为145°.