题目内容
9. 如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )
如图,在平面直角坐标系中,直径为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{4}$个单位长度,则第2016秒时,点P的坐标是( )| A. | (1008,0) | B. | (1008,$\frac{1}{2}$) | C. | (1008,-$\frac{1}{2}$) | D. | (1008π,0) |
分析 设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1($\frac{4n+1}{2}$,$\frac{1}{2}$),P4n+2(2n+1,0),P4n+3($\frac{4n+3}{2}$,-$\frac{1}{2}$),P4n+4(2n+2,0)”,依此规律即可得出结论.
解答 解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1($\frac{1}{2}$,$\frac{1}{2}$),P2(1,0),P3($\frac{3}{2}$,-$\frac{1}{2}$),P4(2,0),P5($\frac{5}{2}$,$\frac{1}{2}$),…,
∴P4n+1($\frac{4n+1}{2}$,$\frac{1}{2}$),P4n+2(2n+1,0),P4n+3($\frac{4n+3}{2}$,-$\frac{1}{2}$),P4n+4(2n+2,0).
∵2016=4×503+4,
∴P2016为(1008,0).
故选A.
点评 本题考查了规律型中的点的坐标,解题的关键是找出变化规律“P4n+1($\frac{4n+1}{2}$,$\frac{1}{2}$),P4n+2(2n+1,0),P4n+3($\frac{4n+3}{2}$,-$\frac{1}{2}$),P4n+4(2n+2,0)”.本题属于中档题,难度不大,解决该题型题目时,根据运动的规律找出点的坐标,根据坐标的变化找出坐标变化的规律是关键.

练习册系列答案
相关题目
20.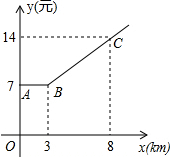 某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
 某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )| A. | 0.71元 | B. | 2.3元 | C. | 1.75元 | D. | 1.4元 |
19.下列说法正确的是( )
| A. | (3,2)和(2,3)表示同一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(-3,1)到x轴的距离为3 |
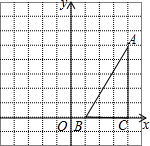 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,再向下平移2个单位,得到△A′B′C′根据所给的直角坐标系(O是坐标原点),解答下列问题:画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标.
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,再向下平移2个单位,得到△A′B′C′根据所给的直角坐标系(O是坐标原点),解答下列问题:画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标.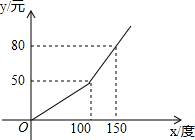 为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量.
为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量. 如图所示,直线AB、CD相交于点O,OE⊥AB,OB平分∠DOF,若∠EOC=110°,求∠BOF,∠COF的度数.
如图所示,直线AB、CD相交于点O,OE⊥AB,OB平分∠DOF,若∠EOC=110°,求∠BOF,∠COF的度数.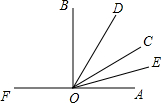 如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.