题目内容
18.先化简,再求值:($\frac{1}{b}$-$\frac{1}{a}$)÷$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$•$\frac{1}{2a+2b}$,其中a=$\sqrt{2}$+1,b=$\sqrt{2}$-1.分析 先将分式进行化简,然后将a与b的值代入即可求出答案.
解答 解:原式=$\frac{a-b}{ab}$•$\frac{(a+b)(a-b)}{(a-b)^{2}}$•$\frac{1}{2(a+b)}$
=$\frac{a-b}{ab}$•$\frac{1}{2(a+b)}$
=$\frac{1}{2ab}$
当a=$\sqrt{2}$+1,b=$\sqrt{2}$-1时,
∴原式=$\frac{1}{2×(2-1)}=\frac{1}{2}$
点评 本题考查分式的化简运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.从2开始,连续的偶数相加,它们和的情况如表:
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=n(n+1);
(2)如下数表是由从1开始的连续自然数组成,观察规律:
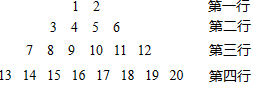
①第n行的第一个数可用含n的式子表示为:n2-n+1;
②如果某行的第一个数为157,求其所在的行数.
| 加数的个数n | S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=15=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)如下数表是由从1开始的连续自然数组成,观察规律:
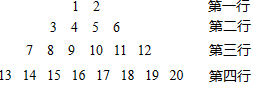
①第n行的第一个数可用含n的式子表示为:n2-n+1;
②如果某行的第一个数为157,求其所在的行数.
10.若二次函数y=(m-1)x2+2x+1的图象与x轴有两个不同的交点,则m的取值范围是( )
| A. | m≤2 | B. | m<2 | C. | m≤2且m≠1 | D. | m<2且m≠1 |
 如图,求证:∠BDC=∠A+∠B+∠C.
如图,求证:∠BDC=∠A+∠B+∠C.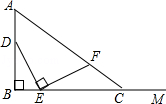 如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=$\frac{1}{2}$DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则y关于x的函数解析式为y=$\frac{12x}{4-x}$(0<x≤2).
如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=$\frac{1}{2}$DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BM于点C,设BE=x,BC=y,则y关于x的函数解析式为y=$\frac{12x}{4-x}$(0<x≤2).