题目内容
17. 如图,在△ABC中,∠C=100°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,求∠APD的度数.
如图,在△ABC中,∠C=100°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,求∠APD的度数.
分析 利用三角形内角和定理,结合角平分线的定义求解.
解答 解:∵∠C=100°,
∴∠ABC+∠BAC=80°,
∴$\frac{1}{2}$(∠BAC+∠ABC)=40°.
∵BD平分∠ABC,AP平分∠BAC,
∴∠APD=∠BAP+∠ABP=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠BAC+∠ABC)=40°.
点评 本题考查三角形的内角和定理和三角形外角的性质.求出∠BAP+∠ABP=$\frac{1}{2}$(∠BAC+∠ABC)=40°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.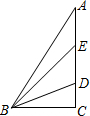 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )| A. | BE是△ABD的中线 | B. | BD是△BCE的角平分线 | ||
| C. | ∠ABE=∠EBD=∠DBC | D. | BC是△ABE的高 |
5.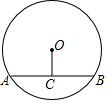 排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
 排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )| A. | 5 | B. | 6 | C. | 8 | D. | 4 |
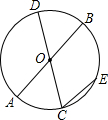 如图,AB、CD是⊙O的直径,弦CE∥AB,$\widehat{AC}$的度数为70°.求∠EOC的度数.
如图,AB、CD是⊙O的直径,弦CE∥AB,$\widehat{AC}$的度数为70°.求∠EOC的度数.